
分析 (1)设等差数列{an}的公差等于d,则由题意可得$\left\{\begin{array}{l}{2{a}_{1}+2d=8}\\{2{a}_{1}+4d=12}\end{array}\right.$,解得 a1=2,d=2,从而得到{an}的通项公式;
(2)由(1)可得 {an}的前n项和为Sn =$\frac{n({a}_{1}+{a}_{n})}{2}$=n(n+1),再由ak+12=a1Sk+3 ,求得正整数k的值.
解答 解:(1)设等差数列{an}的公差等于d,
则由题意可得$\left\{\begin{array}{l}{2{a}_{1}+2d=8}\\{2{a}_{1}+4d=12}\end{array}\right.$,解得a1=2,d=2,
∴{an}的通项公式an =2+2(n-1)=2n;
(2)由(1)可得 {an}的前n项和为Sn=$\frac{n({a}_{1}+{a}_{n})}{2}$=n(n+1),
∵a1,ak+1,Sk+3成等比数列,∴ak+12=a1Sk+3,
∴4(k+1)2 =2(k+3)(k+4),
解得k=5或k=-2(舍去),
故k=5.
点评 本题主要考查等比数列的定义和性质,等差数列的通项公式和求和公式的运用,属于中档题.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
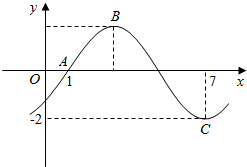 已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
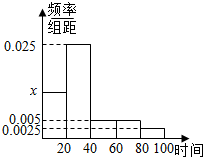 我县某中学为了配备高一新生中寄宿生的用品,招生前随机抽取部分准高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
我县某中学为了配备高一新生中寄宿生的用品,招生前随机抽取部分准高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com