
【题目】在直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2﹣4ρsin(θ![]() )=0.
)=0.
(1)求曲线C的直角坐标方程;
(2)若直线l的参数方程是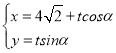 (α为参数),且α∈(
(α为参数),且α∈(![]() ,π)时,直线l与曲线C有且只有一个交点P,求点P的极径.
,π)时,直线l与曲线C有且只有一个交点P,求点P的极径.
 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )的图象为曲线
)的图象为曲线![]() .
.
(Ⅰ)求曲线![]() 上任意一点处的切线的斜率的取值范围;
上任意一点处的切线的斜率的取值范围;
(Ⅱ)若曲线![]() 上存在两点处的切线互相垂直,求其中一条切线与曲线
上存在两点处的切线互相垂直,求其中一条切线与曲线![]() 的切点的横坐标的取值范围;
的切点的横坐标的取值范围;
(Ⅲ)试问:是否存在一条直线与曲线C同时切于两个不同点?如果存在,求出符合条件的所有直线方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l的参数方程为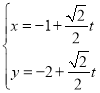 (t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=4acosθ,直线l与曲线C交于不同的两点M,N.
(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=4acosθ,直线l与曲线C交于不同的两点M,N.
(1)求实数a的取值范围;
(2)已知a>0,设点P(﹣1,﹣2),若|PM|,|MN|,|PN|成等比数列,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
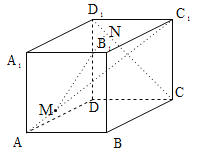
【题目】如图,直四棱柱ABCD﹣A1B1C1D1,底面ABCD是边长为6的正方形,M,N分别为线段AC1,D1C上的动点,若直线MN与平面B1BCC1没有公共点或有无数个公共点,点E为MN的中点,则E点的轨迹长度为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1772年德国的天文学家波得发现了求太阳的行星距离的法则,记地球距离太阳的平均距离为10,可以算得当时已知的六大行星距离太阳的平均距离如下表:
星名 | 水星 | 金星 | 地球 | 火星 | 木星 | 土星 |
与太阳的距离 | 4 | 7 | 10 | 16 | 52 | 100 |
除水星外,其余各星与太阳的距离都满足波得定则(某一数列规律),当时德国数学家高斯根据此定则推算,火星和木星之间距离太阳28还有一颗大行星,1801年,意大利天文学家皮亚齐经过观测,果然找到了火星和木星之间距离太阳28的谷神星以及它所在的小行星带,请你根据这个定则,估算从水星开始由近到远算,第10个行星与太阳的平均距离大约是( )
A.388B.772C.1540D.3076
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,抛物线
,抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的上顶点,且
的上顶点,且![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上的射影依次为
上的射影依次为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() ,当
,当![]() 变化时,证明:
变化时,证明: ![]() 为定值;
为定值;
(3)当![]() 变化时,直线
变化时,直线![]() 与
与![]() 是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年国际乒联总决赛在韩国仁川举行,比赛时间为12月13﹣12月16日,在男子单打项目,中国队准备选派4人参加.已知国家一线队共6名队员,二线队共4名队员.
(1)求恰好有3名国家一线队队员参加比赛的概率;
(2)设随机变量X表示参加比赛的国家二线队队员的人数,求X的分布列;
(3)男子单打决赛是林高远(中国)对阵张本智和(日本),比赛采用七局四胜制,已知在每局比赛中,林高远获胜的概率为![]() ,张本智和获胜的概率为
,张本智和获胜的概率为![]() ,前两局比赛双方各胜一局,且各局比赛的结果相互独立,求林高远获得男子单打冠军的概率.
,前两局比赛双方各胜一局,且各局比赛的结果相互独立,求林高远获得男子单打冠军的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com