
【题目】已知△ABC的面积为8,cosA= ![]() ,D为BC上一点,
,D为BC上一点, ![]() =
= ![]() +
+ ![]() ,过点D做AB,AC的垂线,垂足分别为E,F,则
,过点D做AB,AC的垂线,垂足分别为E,F,则 ![]()
![]() = .
= .
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆 ![]() 的离心率为
的离心率为 ![]() ,直线y=x被椭圆C截得的线段长为
,直线y=x被椭圆C截得的线段长为 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过原点的直线与椭圆C交于两点(A,B不是椭圆C的顶点),点D在椭圆C上,且AD⊥AB,直线BD与x轴、y轴分别交于M,N两点.设直线BD,AM斜率分别为k1 , k2 , 证明存在常数λ使得k1=λk2 , 并求出λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三个内角A,B,C的对边分别是a,b,c,则: ①若cosBcosC>sinBsinC,则△ABC一定是钝角三角形;
②若acosA=bcosB,则△ABC为等腰三角形;
③ ![]() ,
, ![]() ,若
,若 ![]() ,则△ABC为锐角三角形;
,则△ABC为锐角三角形;
④若O为△ABC的外心, ![]() ;
;
⑤若sin2A+sin2B=sin2C, ![]() ,
, 
以上叙述正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C: ![]() +
+ ![]() =1(a>b>0),定义椭圆的“伴随圆”方程为x2+y2=a2+b2;若抛物线x2=4y的焦点与椭圆C的一个短轴重合,且椭圆C的离心率为
=1(a>b>0),定义椭圆的“伴随圆”方程为x2+y2=a2+b2;若抛物线x2=4y的焦点与椭圆C的一个短轴重合,且椭圆C的离心率为 ![]() .
.
(1)求椭圆C的方程和“伴随圆”E的方程;
(2)过“伴随圆”E上任意一点P作椭圆C的两条切线PA,PB,A,B为切点,延长PA与“伴随圆”E交于点Q,O为坐标原点.
①证明:PA⊥PB;
②若直线OP,OQ的斜率存在,设其分别为k1 , k2 , 试判断k1k2是否为定值,若是,求出该值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,正确的有__________.
①如果![]() 、
、![]() 与平面
与平面![]() 共面且
共面且![]() ,
,![]() ,那么
,那么![]() 就是平面
就是平面![]() 的一个法向量;
的一个法向量;
②设![]() :实数
:实数![]() ,
,![]() 满足
满足![]() ;
;![]() :实数
:实数![]() ,
,![]() 满足
满足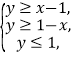 则
则![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
③已知椭圆![]() 与双曲线
与双曲线![]() 的焦点重合,
的焦点重合,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的离心率,则
的离心率,则![]() ,且
,且![]() ;
;
④菱形是圆的内接四边形或是圆的外切四边形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P(x0 , y0)是椭圆 ![]() +y2=1的上的点,l是椭圆在点P处的切线,O是坐标原点,OQ∥l与椭圆的一个交点是Q,P,Q都在x轴上方
+y2=1的上的点,l是椭圆在点P处的切线,O是坐标原点,OQ∥l与椭圆的一个交点是Q,P,Q都在x轴上方
(1)当P点坐标为( ![]() ,
, ![]() )时,利用题后定理写出l的方程,并验证l确定是椭圆的切线;
)时,利用题后定理写出l的方程,并验证l确定是椭圆的切线;
(2)当点P在第一象限运动时(可以直接应用定理)
①求△OPQ的面积
②求直线PQ在y轴上的截距的取值范围.
定理:若点(x0 , y0)在椭圆 ![]() +y2=1上,则椭圆在该点处的切线方程为
+y2=1上,则椭圆在该点处的切线方程为 ![]() +y0y=1.
+y0y=1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,SA⊥底面ABC,AC=AB=SA=2,AC⊥AB,D,E分别是AC,BC的中点,F在SE上,且SF=2FE. 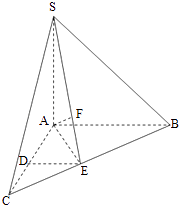
(1)求证:AF⊥平面SBC;
(2)在线段上DE上是否存在点G,使二面角G﹣AF﹣E的大小为30°?若存在,求出DG的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长郡中学早上8点开始上课,若学生小典与小方匀在早上7:40至8:00之间到校,且两人在该时间段的任何时刻到校都是等可能的,则小典比小方至少早5分钟到校的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,侧棱PA⊥平面ABCD,E为AD的中点,BE∥CD,BE⊥AD,PA=AE=BE=2,CD=1; 
(1)求二面角C﹣PB﹣E的余弦值;
(2)在线段PE上是否存在点M,使得DM∥平面PBC?若存在,求出点M的位置,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com