
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 上位于第一象限内的任意一点,
上位于第一象限内的任意一点,![]() 为坐标原点,
为坐标原点,![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,![]() ,圆
,圆![]() :
:![]() .
.

(1)求椭圆![]() 和圆
和圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作
作![]() 与圆
与圆![]() 相切于点
相切于点![]() ,使得点
,使得点![]() ,点
,点![]() 在
在![]() 的两侧.求四边形
的两侧.求四边形![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】某校为了诊断高三学生在市“一模”考试中文科数学备考的状况,随机抽取了50名学生的市“一模”数学成绩进行分析,将这些成绩分为九组,第一组[60,70),第二组[70,80),……,第九组[140,150],并绘制了如图所示的频率分布直方图.

(1)试求出![]() 的值并估计该校文科数学成绩的众数和中位数;
的值并估计该校文科数学成绩的众数和中位数;
(2)现从成绩在[120,150]的同学中随机抽取2人进行谈话,那么抽取的2人中恰好有一人的成绩在[130,140)中的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“文、明、中、国”四个字,有放回地从中任取一个小球,直到“中”“国”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“文、明、中、国”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下18组随机数:
232 321 230 023 123 021 132 220 001
231 130 133 231 013 320 122 103 233
由此可以估计,恰好第三次就停止的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过M(![]() ,1),N(
,1),N(![]() ,1)两点,且圆心C在直线x+y﹣3=0上,过点A(﹣1,0)的动直线l与圆C相交于P、Q两点.
,1)两点,且圆心C在直线x+y﹣3=0上,过点A(﹣1,0)的动直线l与圆C相交于P、Q两点.
(Ⅰ)求圆C的方程;
(Ⅱ)当|PQ|=4![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有![]() 名学生排成一排,求分别满足下列条件的排法种数,要求列式并给出计算结果.
名学生排成一排,求分别满足下列条件的排法种数,要求列式并给出计算结果.
(1)甲不在两端;
(2)甲、乙相邻;
(3)甲、乙、丙三人两两不得相邻;
(4)甲不在排头,乙不在排尾。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 是椭圆
是椭圆![]() :
:![]() 的左右焦点,焦距为6,椭圆
的左右焦点,焦距为6,椭圆![]() 上存在点
上存在点![]() 使得
使得![]() ,且
,且![]() 的面积为9.
的面积为9.

(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 轴不重合,
轴不重合,![]() 是
是![]() 轴上一点,且
轴上一点,且![]() ,求点
,求点![]() 纵坐标的取值集合.
纵坐标的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某种细菌的适宜生长温度为![]() ,为了研究该种细菌的繁殖数量
,为了研究该种细菌的繁殖数量![]() (单位:个)随温度
(单位:个)随温度![]() (单位:
(单位:![]() )变化的规律,收集数据如下:
)变化的规律,收集数据如下:
温度 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
繁殖数量 | 20 | 25 | 33 | 27 | 51 | 112 | 194 |
对数据进行初步处理后,得到了一些统计量的值,如下表所示:
|
|
|
|
|
|
|
18 | 66 | 3.8 | 112 | 4.3 | 1428 | 20.5 |
其中![]() ,
,![]() .
.
(1)请绘出![]() 关于
关于![]() 的散点图,并根据散点图判断
的散点图,并根据散点图判断![]() 与
与![]() 哪一个更适合作为该种细菌的繁殖数量
哪一个更适合作为该种细菌的繁殖数量![]() 关于
关于![]() 的回归方程类型(结果精确到0.1);
的回归方程类型(结果精确到0.1);
(2)当温度为![]() 时,该种细菌的繁殖数量的预报值为多少?
时,该种细菌的繁殖数量的预报值为多少?
参考公式:对于一组数据![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: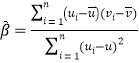 ,
,![]() .参考数据:
.参考数据:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com