
【题目】函数f(x)= ![]() 的定义域为( )
的定义域为( )
A.(﹣∞,11)
B.(1,11]
C.(1,11)
D.(1,+∞)
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,A(1,1),B(2,0),| ![]() |=1.
|=1.
(1)求 ![]() 与
与 ![]() 夹角;
夹角;
(2)若 ![]() 与
与 ![]() 垂直,求点C的坐标;
垂直,求点C的坐标;
(3)求| ![]() +
+ ![]() +
+ ![]() |的取值范围.
|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验.为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.
分数 |
|
|
|
|
|
甲班频数 | 5 | 6 | 4 | 4 | 1 |
一般频数 | 1 | 3 | 6 | 5 | 5 |
(1)由以下统计数据填写下面![]() 列联表,并判断能否在犯错误的额概率不超过0.025的前提下认为“成绩优良与教学方式有关”?
列联表,并判断能否在犯错误的额概率不超过0.025的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
附:![]() ,其中
,其中![]() .
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核.在这8人中,记成绩不优良的乙班人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,E,F,P,Q分别是BC,C1D1 , AD1 , BD的中点. 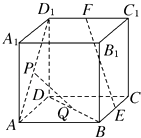
(1)求证:PQ∥平面DCC1D1;
(2)求PQ的长;
(3)求证:EF∥平面BB1D1D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A,B,C所对的边分别为a,b,c,S表示三角形的面积,若asinA+bsinB=csinC,且S= ![]() ,则对△ABC的形状的精确描述是( )
,则对△ABC的形状的精确描述是( )
A.直角三角形
B.等腰三角形
C.等腰或直角三角形
D.等腰直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x|x+bx+c,给出下列4个命题:
①b=0,c>0时,方程f(x)=0只有一个实数根;
②c=0时,y=f(x)是奇函数;
③y=f(x)的图象关于点(0,c)对称;
④方程f(x)=0至多有2个不相等的实数根.
上述命题中的所有正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,已知a1=1,a2=2,an+2= ![]() (k∈N*).
(k∈N*).
(1)求数列{an}的通项公式;
(2)求满足2an+1=an+an+2的正整数n的值;
(3)设数列{an}的前n项和为Sn , 问是否存在正整数m,n,使得S2n=mS2n﹣1?若存在,求出所有的正整数对(m,n);若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com