
【题目】一个圆柱形圆木的底面半径为1 m,长为10 m,将此圆木沿轴所在的平面剖成两部分.现要把其中一部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设![]() ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).

(1)求V关于θ的函数表达式;
(2)求![]() 的值,使体积V最大;
的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(2)当![]() 时,是否存在正实数
时,是否存在正实数![]() ,当
,当![]() (
(![]() 是自然对数底数)时,函数
是自然对数底数)时,函数![]() 的最小值是3,若存在,求出
的最小值是3,若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有![]() 个形状大小完全相同的小球,球的编号分别为
个形状大小完全相同的小球,球的编号分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(![]() )若从袋中每次随机抽取
)若从袋中每次随机抽取![]() 个球,有放回的抽取
个球,有放回的抽取![]() 次,求取出的两个球编号之和为
次,求取出的两个球编号之和为![]() 的概率.
的概率.
(![]() )若从袋中每次随机抽取
)若从袋中每次随机抽取![]() 个球,有放回的抽取
个球,有放回的抽取![]() 次,求恰有
次,求恰有![]() 次抽到
次抽到![]() 号球的概率.
号球的概率.
(![]() )若一次从袋中随机抽取
)若一次从袋中随机抽取![]() 个球,求球的最大编号为
个球,求球的最大编号为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方体ABCD-A1B1C1D1的棱长为3,M,N分别是棱AA1,AB上的点,且AM=AN=1.
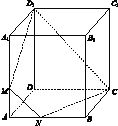
(1)证明:M,N,C,D1四点共面;
(2)平面MNCD1将此正方体分为两部分,求这两部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
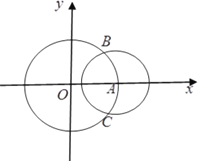
【题目】如图,在平面直角坐标系![]() 中,圆
中,圆![]() :
:![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,以点
,以点![]() 为圆心的圆
为圆心的圆![]() :
:![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() 的长;
的长;
(2)当![]() 变化时,求
变化时,求![]() 的最小值;
的最小值;
(3)过点![]() 的直线
的直线![]() 与圆A切于点
与圆A切于点![]() ,与圆
,与圆![]() 分别交于点
分别交于点![]() ,
,![]() ,若点
,若点![]() 是
是![]() 的中点,试求直线
的中点,试求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年,京津冀等地数城市指数“爆表”,尤其2015年污染最重.为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与PM2.5的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
PM2.5的浓度y(微克/立方米) | 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(Ⅰ)由散点图知y与x具有线性相关关系,求y关于x的线性回归方程;
(Ⅱ)(ⅰ)利用(Ⅰ)所求的回归方程,预测该市车流量为8万辆时PM2.5的浓度;
(ⅱ)规定:当一天内PM2.5的浓度平均值在(0,50]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(50,100]内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
参考公式:回归直线的方程是![]() ,其中
,其中 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是![]() ,D是AC的中点。
,D是AC的中点。

(1)求证:B1C∥平面A1BD;
(2)求二面角A1-BD-A的大小;
(3)在线段AA1上是否存在一点E,使得平面B1C1E⊥平面A1BD,若存在,求出AE的长;若不存在,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com