
分析 首先将函数化为:y=(x-1)+$\frac{10}{x-1}$-2,再用基本不等式和双勾函数的性质求最值.
解答 解:y=f(x)=$\frac{{x}^{2}-4x+13}{x-1}$=$\frac{(x-1)^2-2(x-1)+10}{x-1}$=(x-1)+$\frac{10}{x-1}$-2,
∵x∈[2,5],∴x-1∈[1,4],
根据基本不等式,(x-1)+$\frac{10}{x-1}$≥2$\sqrt{(x-1)•\frac{10}{x-1}}$=2$\sqrt{10}$,
当且仅当:(x-1)=$\frac{10}{x-1}$,解得x=$\sqrt{10}$+1∈[2,5],
所以,ymin=2$\sqrt{10}$-2,
再根据双勾函数的性质,ymax=max{f(2),f(5)},
其中,f(2)=9,f(5)=$\frac{9}{2}$,所以ymax=9,
所以该函数的值域为:[2$\sqrt{10}$-2,9].
故答案为:[2$\sqrt{10}$-2,9].
点评 本题主要考查了函数值域的求法,涉及双勾函数的性质,以及运用基本不等式最值,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{21}^{17}$ | B. | C${\;}_{21}^{17}$-1 | C. | C${\;}_{21}^{18}$-1 | D. | C${\;}_{21}^{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
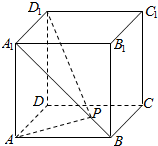
| A. | 2 | B. | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ | C. | $2+\sqrt{2}$ | D. | $\sqrt{2+\sqrt{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com