
半径为1的球面上有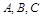 三点,其中点
三点,其中点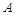 与
与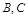 两点间的球面距离均为
两点间的球面距离均为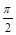 ,
,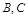 两点间的球面距离为
两点间的球面距离为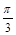 ,则球心到平面
,则球心到平面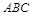 的距离为( )
的距离为( )
A.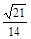 B.
B.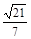 C.
C. D.
D.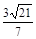
B
【解析】
试题分析:根据题意可知:球心O与A,B,C三点构成三棱锥O-ABC,且OA=OB=OC=R=1,∠AOB=∠AOC=90°,∠BOC=60°,故AO⊥面BOC.所以此题可以根据体积法求得球心O到平面ABC的距离. 解:球心O与A,B,C三点构成三棱锥O-ABC,如图所示,
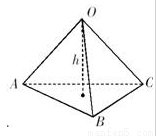
已知OA=OB=OC=R=1,∠AOB=∠AOC=90°,∠BOC=60°,由此可得AO⊥面BOC.∵S△BOC=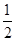 ,S△ABC=
,S△ABC=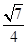 .
.
∴由VA-BOC=VO-ABC,得 h=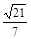 .故选B.
.故选B.
考点:点到面的距离, 球面距离
点评:本小题主要考查立体几何球面距离及点到面的距离、三棱锥的结构等基础知识,考查运算求解能力,考查空间想象力.属于基础题


科目:高中数学 来源:2010年普通高等学校招生全国统一考试(重庆卷)数学文史类模拟试卷(二) 题型:选择题
半径为1的球面上有三点A、B、C,其中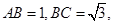 A、C两点间的球面距离为
A、C两点间的球面距离为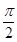 ,则球心到平面ABC的距离为
,则球心到平面ABC的距离为
A. 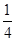 B.
B.
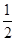 C.
C.
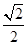 D.
D.
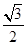
查看答案和解析>>
科目:高中数学 来源:2010-2011年广西北海市合浦县教育局高二下期末考数学试卷 题型:选择题
半径为1的球面上有三点A、B、C,A和B与A和C之间的球面距离都是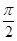 ,B
,B
和C之间的球面距离是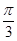 ,则过A、B、C三点的截面到球心的距离是
,则过A、B、C三点的截面到球心的距离是
A. 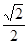 B.
B.
 C.
C.
 D.
D.
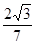
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com