
(本题满分9分)
设平面上向量 =(cosα,sinα) (0°≤α<360°),
=(cosα,sinα) (0°≤α<360°), =(-
=(- ,
, ).
).
(1)试证:向量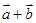 与
与 垂直;
垂直;
(2)当两个向量 与
与 的模相等时,求角α.
的模相等时,求角α.
(1)见解析;(2)α=30°,或α=210°.
【解析】本试题主要是考查了向量的数量积的运算,以及向量的数量积的性质的运用,以及三角函数的变形运用,和三角方程的求解的综合试题。
((1)根据已知要证明向量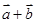 与
与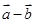 垂直,则利用数量积为零即可。
垂直,则利用数量积为零即可。
(2)由|a|=1,|b|=1,且|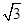 a+b|=|a-
a+b|=|a-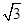 b|,利用模相等,则平方后相等来解得关于角α的方程,然后解三角方程得到角的值。
b|,利用模相等,则平方后相等来解得关于角α的方程,然后解三角方程得到角的值。
解: (1)(a+b)·(a-b)=(cosα-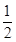 ,sinα+
,sinα+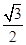 )·(cosα+
)·(cosα+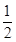 ,sinα-
,sinα-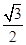 )
)
=(cosα-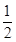 )(cosα+
)(cosα+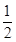 )+(sinα+
)+(sinα+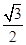 )(sinα-
)(sinα-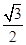 )
)
=cos2α-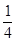 +sin2α-
+sin2α-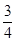 =0,
=0,
∴(a+b)⊥(a-b). ……4分
(2)由|a|=1,|b|=1,且|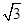 a+b|=|a-
a+b|=|a-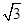 b|,平方得(
b|,平方得(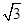 a+b)2=(a-
a+b)2=(a-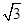 b)2,
b)2,
整理得2a2-2b2+4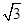 ab=0①.
ab=0①.
∵|a|=1,|b|=1,∴①式化简得a·b=0,
a·b=(cosα,sinα)·(-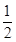 ,
,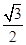 )=-
)=-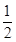 cosα+
cosα+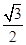 sinα=0,即cos(60°+α)=0.
sinα=0,即cos(60°+α)=0.
∵0°≤α<360°,∴可得α=30°,或α=210°. ……9分


科目:高中数学 来源:2011-2012学年上海市闵行区高三上学期期末质量抽测理科数学试卷 题型:解答题
(本题满分14分)本题共有2个小题,第(1)小题满分5分,第(2)小题满分9分.
设双曲线 ,
, 是它实轴的两个端点,
是它实轴的两个端点, 是其虚轴的一个端点.已知其一条渐近线的一个方向向量是
是其虚轴的一个端点.已知其一条渐近线的一个方向向量是 ,
, 的面积是
的面积是 ,
, 为坐标原点,直线
为坐标原点,直线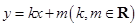 与双曲线C相交于
与双曲线C相交于 、
、 两点,且
两点,且 .
.
(1)求双曲线 的方程;
的方程;
(2)求点 的轨迹方程,并指明是何种曲线.
的轨迹方程,并指明是何种曲线.
查看答案和解析>>
科目:高中数学 来源:浙江省台州市09-10学年高一下学期期末质量评估数学试题 题型:解答题
(本题满分9分)在平面直角坐标系 中,已知直线
中,已知直线 被圆
被圆
 截得的弦长为
截得的弦长为 .
.
(1)求圆 的方程;
的方程;
(2)设圆 和
和 轴相交于
轴相交于 ,
, 两点,点
两点,点 为圆
为圆 上不同于
上不同于 ,
, 的任意一点,直线
的任意一点,直线 ,
, 交
交 轴于
轴于 ,
, 两点.当点
两点.当点 变化时,以
变化时,以 为直径的圆
为直径的圆 是否经过圆
是否经过圆 内一定点?请证明你的结论;
内一定点?请证明你的结论;
(3)若 的顶点
的顶点 在直线
在直线 上,
上, ,
, 在圆
在圆 上,且直线
上,且直线 过圆心
过圆心 ,
, ,求点
,求点 的纵坐标的范围.高.考.资.源.网
的纵坐标的范围.高.考.资.源.网
查看答案和解析>>
科目:高中数学 来源:2011年安徽省高一第一学期期中考试数学 题型:解答题
.(本题满分9分)
已知:函数 对一切实数
对一切实数 都有
都有
 成立,且
成立,且 .(1)求
.(1)求 的值 (2)求
的值 (2)求 的解析式
的解析式
(3)已知 ,设P:当
,设P:当 时,不等式
时,不等式 恒成立;Q:当
恒成立;Q:当 时,
时, 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的 的集合记为
的集合记为 ,满足Q成立的
,满足Q成立的 的集合记为
的集合记为 ,求
,求 ∩
∩ (
( 为全集)
为全集)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com