
 +y2=1上的点,M(m,0)(m>0)是定点,若|MP|的最小值等于
+y2=1上的点,M(m,0)(m>0)是定点,若|MP|的最小值等于 ,则m=________.
,则m=________. 或
或 +
+
 x2-2mx+1+m2,因为抛物线y=F(x)关于直线直线x=2m对称,且P点横坐标x∈[-
x2-2mx+1+m2,因为抛物线y=F(x)关于直线直线x=2m对称,且P点横坐标x∈[-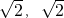 ],所以分2m>
],所以分2m> 和2m≤
和2m≤ 两种情况,分别对F(x)的最小值为
两种情况,分别对F(x)的最小值为 进行讨论,解之即可得到实数m的值,从而得到本题答案.
进行讨论,解之即可得到实数m的值,从而得到本题答案. +y2=1上的点,
+y2=1上的点, ,由此可得|MP|2=(x-m)2+y2=(x-m)2+(1-
,由此可得|MP|2=(x-m)2+y2=(x-m)2+(1- ),
), x2-2mx+1+m2,
x2-2mx+1+m2,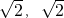 ]
] 时,即m>
时,即m> 时,F(x)在[-
时,F(x)在[-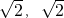 ]上为减函数,
]上为减函数, )=m2-2
)=m2-2 m+2=(
m+2=( )2,解之得m=
)2,解之得m= +
+ (负值舍去)
(负值舍去) 时,即0<m≤
时,即0<m≤ 时,F(x)在[-
时,F(x)在[- ,2m]上为减函数,在[2m,
,2m]上为减函数,在[2m, ]上为增函数,
]上为增函数, )2,解之得m=
)2,解之得m= (负值舍去).
(负值舍去). 或
或 +
+
 或
或 +
+


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com