
分析 (1)当0≤x≤10时,Q(x)=$\frac{{x}^{2}}{16}+\frac{x}{4}+\frac{5}{4}$,依题意:Q(x)=$\frac{{x}^{2}}{16}+\frac{x}{4}+\frac{5}{4}$≤5,即可求出该工艺处理量x的取值范围;
(2)分类求最值,即可得出结论.
解答 解:(1)设该企业计划在A国投入的总成本为Q(x)(亿元),
则当0≤x≤10时,Q(x)=$\frac{{x}^{2}}{16}+\frac{x}{4}+\frac{5}{4}$,
依题意:Q(x)=$\frac{{x}^{2}}{16}+\frac{x}{4}+\frac{5}{4}$≤5,
即x2+4x-60≤0,解得-10≤x≤6,
结合条件0≤x≤10,∴0≤x≤6…(3分)
(2)依题意,该企业计划在A国投入的总成本当0≤x≤10时,Q(x)=$\frac{{x}^{2}}{16}+\frac{x}{4}+\frac{5}{4}$,
当x>10时,Q(x)=x+$\frac{4}{x}$-$\frac{2}{5}$,
则平均处理成本①当0≤x≤10时,$\frac{Q(x)}{x}$=$\frac{x}{16}+\frac{5}{4x}$+$\frac{1}{4}$≥$\frac{\sqrt{5}+1}{4}$,当且仅当$\frac{x}{16}=\frac{5}{4x}$,
即x=2$\sqrt{5}$时,$\frac{Q(x)}{x}$的最小值为$\frac{\sqrt{5}+1}{4}$,…(7分)
②当x>10时,$\frac{Q(x)}{x}$═4($\frac{1}{x}$-$\frac{1}{20}$)2+$\frac{99}{100}$,
∴当$\frac{1}{x}$=$\frac{1}{20}$,即x=20时,$\frac{Q(x)}{x}$的最小值为$\frac{99}{100}$>$\frac{\sqrt{5}+1}{4}$,
∴当x=2$\sqrt{5}$时,$\frac{Q(x)}{x}$的最小值为$\frac{\sqrt{5}+1}{4}$,…(11分)
答:(Ⅰ)该工艺处理量x的取值范围是0≤x≤6.
(Ⅱ)该企业处理量为22$\sqrt{5}$万吨时,才能使每万吨的平均处理成本最低,平均处理成本最低为$\frac{\sqrt{5}+1}{4}$亿元…(12分)
点评 本题考查利用数学知识解决实际问题,考查基本不等式的运用,考查二次函数的性质,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
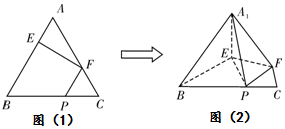 在边长为3的正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图(1)将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图(2)).
在边长为3的正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图(1)将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图(2)).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com