
分析 取AC的中点P,连结PM、PN,则∠MPN为AB与CD所成的角(或所成的角的补角),∠PMN是AB与MN所成的角(或所成角的补角),由此能求出直线AB与MN所成的角.
解答 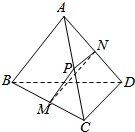 解:如图,取AC的中点P,连结PM、PN,
解:如图,取AC的中点P,连结PM、PN,
则PM∥AB,且PM=$\frac{1}{2}AB$,PN∥CD,且PN=$\frac{1}{2}CD$,
∴∠MPN为AB与CD所成的角(或所成的角的补角),
∴∠MPN=60°或∠MPN=120°,
若∠MPN=60°,∵PM∥AB,∴∠PMN是AB与MN所成的角(或所成角的补角),
又∵AB=CD,∴PM=PN《
∴△PMN是等边三角形,∴∠PMN=60°,
∴AB与MN所成的角为60°;
若∠MPN=120°,则△PMN是等腰三角形,∴∠PMN=30°,
∴AB与MN所成的角为30°,
∴直线AB与MN所成的角为60°或30°.
点评 本题考查异面直线所成角的大小的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}(\overrightarrow a-\overrightarrow b)$ | B. | $\frac{1}{2}(\overrightarrow a+\overrightarrow b)$ | C. | $\frac{1}{2}(\overrightarrow b-\overrightarrow a)$ | D. | $\frac{1}{2}\overrightarrow a-\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
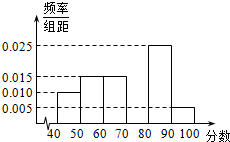 某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(满分100分,均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.根据图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(满分100分,均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.根据图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ρ=2$\sqrt{2}$sin(θ+$\frac{π}{4}$) | B. | ρ=2$\sqrt{2}$sin(θ-$\frac{π}{4}$) | C. | ρ=2$\sqrt{2}$cos(θ+$\frac{π}{4}$) | D. | ρ=-2$\sqrt{2}$cos(θ-$\frac{π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com