
【题目】已知函数f(x)=ln(x+2a)﹣ax,a>0.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)记f(x)的最大值为M(a),若a2>a1>0且M(a1)=M(a2),求证: ![]() ;
;
(Ⅲ)若a>2,记集合{x|f(x)=0}中的最小元素为x0 , 设函数g(x)=|f(x)|+x,求证:x0是g(x)的极小值点.
【答案】解:(Ⅰ):f′(x)= ![]() ﹣a=
﹣a= 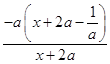 ,
,
∵x>﹣2a,a>0,
由f′(x)>0,得﹣2a<x< ![]() ﹣2a,
﹣2a,
由f′(x)<0,得x> ![]() ﹣2a,
﹣2a,
∴f(x)的增区间为(﹣2a, ![]() ﹣2a),减区间为(
﹣2a),减区间为( ![]() ﹣2a,+∞),
﹣2a,+∞),
(Ⅱ)由(Ⅰ)知,M(a)=f( ![]() ﹣2a)=2a2﹣1﹣lna,
﹣2a)=2a2﹣1﹣lna,
∴2a12﹣1﹣lna1=2a22﹣1﹣lna2,
∴2(a22﹣a12)=lna2﹣lna1=ln ![]() ,
,
∴2a1a2![]() =ln
=ln ![]() ,
,
∴4a1a2( ![]() ﹣
﹣ ![]() )=2ln
)=2ln ![]() ,
,
∴4a1a2=  ,
,
设h(t)=t﹣ ![]() ﹣2lnt,t>1
﹣2lnt,t>1
∴h′(t)=1+ ![]() ﹣
﹣ ![]() =(1﹣
=(1﹣ ![]() )2>0,
)2>0,
∴h(x)在(1,+∞)单调递增,h(t)>h(1)=0,
即t﹣ ![]() >2lnt>0,
>2lnt>0,
∵ ![]() >1,
>1,
∴ ![]() ﹣
﹣ ![]() >2ln
>2ln ![]() >0,
>0,
∴  <1,
<1,
∴a1a2< ![]() ;
;
(Ⅲ)由(Ⅰ)可知,f(x)在区间(﹣2a, ![]() ﹣2a),
﹣2a),
又x→﹣2a时,f(x)→﹣∞,
易知f( ![]() ﹣2a)=M(a)=2a2﹣1﹣lna在(2,+∞)递增,
﹣2a)=M(a)=2a2﹣1﹣lna在(2,+∞)递增,
M(a)>M(2)=7﹣ln2>0,
∴﹣2a<x0< ![]() ﹣2a,且﹣2a<x<x0,f(x)<0,
﹣2a,且﹣2a<x<x0,f(x)<0,
x0<x< ![]() ﹣2a时,f(x)>0,
﹣2a时,f(x)>0,
∴当﹣2a<x< ![]() ﹣2a时,g(x)=
﹣2a时,g(x)= 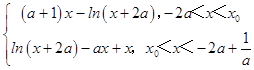 ,
,
于是﹣2a<x<x0时,g′(x)=(a+1)﹣ ![]() <a+1﹣
<a+1﹣ ![]() ,
,
∴若能证明x0< ![]() ﹣2a,便能证明(a+1)﹣
﹣2a,便能证明(a+1)﹣ ![]() <0,
<0,
记φ(a)=f( ![]() ﹣2a)=2a2+
﹣2a)=2a2+ ![]() ﹣1﹣ln(a+1),
﹣1﹣ln(a+1),
∴φ(a)=4a﹣ ![]() ﹣
﹣ ![]() ,
,
∵a>2,
∴h′(a)>8﹣ ![]() >0,
>0,
∴φ(a)在(2,+∞)上单调递增,
∴φ(a)>φ(2)= ![]() ﹣ln3>0,
﹣ln3>0,
∵ ![]() ﹣2a<
﹣2a< ![]() ﹣2a,
﹣2a,
∴f(x)在(﹣2a, ![]() ﹣2a)内单调递减,
﹣2a)内单调递减,
∴x0∈(﹣2a, ![]() ﹣2a),
﹣2a),
于是﹣2a<x<x0时,g′(x)=a+1﹣ ![]() <a+1﹣
<a+1﹣ 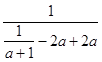 =0,
=0,
∴g(x)在(﹣2a,x0)递减,
当x0<x< ![]() ﹣2a时,相应的g′(x)=
﹣2a时,相应的g′(x)= ![]() ﹣(a﹣1)>
﹣(a﹣1)> 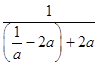 ﹣(a﹣1)=1>0,
﹣(a﹣1)=1>0,
∴g(x)在(x0, ![]() ﹣2a)递增,
﹣2a)递增,
故x0是g(x)的极小值点.
【解析】(Ⅰ)先求导,根据导数和函数单调性的关系即可得到函数的单调区间,(Ⅱ)由(Ⅰ)知,M(a)=f( ![]() ﹣2a)=2a2﹣1﹣lna,继而得到2a12﹣1﹣lna1=2a22﹣1﹣lna2,通过转化得到4a1a2=
﹣2a)=2a2﹣1﹣lna,继而得到2a12﹣1﹣lna1=2a22﹣1﹣lna2,通过转化得到4a1a2= ![]() ,设h(t)=t﹣
,设h(t)=t﹣ ![]() ﹣2lnt,t>1根据函数的单调性证明
﹣2lnt,t>1根据函数的单调性证明 ![]() <1,问题即可得以证明,(Ⅲ)由(Ⅰ)可得,g(x)=
<1,问题即可得以证明,(Ⅲ)由(Ⅰ)可得,g(x)= 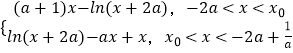 ,分类讨论,得到g(x)在(﹣2a,x0)递减,g(x)在(x0,
,分类讨论,得到g(x)在(﹣2a,x0)递减,g(x)在(x0, ![]() ﹣2a)递增,故x0是g(x)的极小值点.
﹣2a)递增,故x0是g(x)的极小值点.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】设a,b∈R,函数 ![]() ,g(x)=ex(e为自然对数的底数),且函数f(x)的图象与函数g(x)的图象在x=0处有公共的切线.
,g(x)=ex(e为自然对数的底数),且函数f(x)的图象与函数g(x)的图象在x=0处有公共的切线.
(Ⅰ)求b的值;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)若g(x)>f(x)在区间(﹣∞,0)内恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,面ABB1A1为矩形,AB=1,AA1= ![]() ,D为AA1的中点,BD与AB1交于点O,CO⊥面ABB1A1
,D为AA1的中点,BD与AB1交于点O,CO⊥面ABB1A1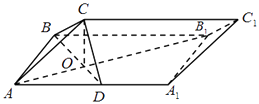
(Ⅰ)证明:BC⊥AB1
(Ⅱ)若OC=OA,求二面角A﹣BC﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列两个命题: 命题p::若在边长为1的正方形ABCD内任取一点M,则|MA|≤1的概率为 ![]() .命题q:设
.命题q:设 ![]() ,
, ![]() 是两个非零向量,则“
是两个非零向量,则“ ![]() =|
=| ![]() |”是“
|”是“ ![]() 与
与 ![]() 共线”的充分不必要条件,那么,下列命题中为真命题的是( )
共线”的充分不必要条件,那么,下列命题中为真命题的是( )
A.p∧q
B.¬p
C.p∧(¬q)
D.(¬p)∨(q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前项和为Sn , 且 ![]() ,用[x]表示不超过x的最大整数,如[﹣0.1]=﹣1,[1.6]=1,设bn=[an],则数列{bn}的前2n项和b1+b2+b3+b4++b2n﹣1+b2n= .
,用[x]表示不超过x的最大整数,如[﹣0.1]=﹣1,[1.6]=1,设bn=[an],则数列{bn}的前2n项和b1+b2+b3+b4++b2n﹣1+b2n= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A.3600
B.1080
C.1440
D.2520
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax,g(x)= ![]() +a.
+a.
(1)当a=2 时,求F(x)=f(x)﹣g(x)在(0,2]的最大值;
(2)讨论函数F(x)=f(x)﹣g(x) 的单调性;
(3)若f(x)g(x)≤0 在定义域内恒成立,求实数a的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】习大大构建的“一带一路”经济带的发展规划已经得到了越来越多相关国家的重视和参与.某市顺潮流、乘东风,闻迅而动,决定利用旅游资源优势,撸起袖子大干一场.为了了解游客的情况,以便制定相应的策略.在某月中随机抽取甲、乙两个景点各10天的游客数,画出茎叶图如下: 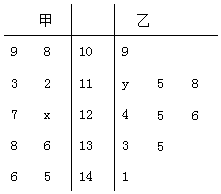
(1)若景点甲中的数据的中位数是125,景点乙中的数据的平均数是124,求x,y的值;
(2)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据.今从这段时期中任取4天,记其中游客数超过120人的天数为ξ,求概率P(ξ≤2);
(3)现从上图的共20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于115且不高于125人的天数为η,求η的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com