
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (t为参数,
(t为参数,![]() ).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知直线L的极坐标方程为
).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知直线L的极坐标方程为![]() .
.
(1)设P是曲线C上的一个动点,当![]() 时,求点P到直线l的距离的最大值;
时,求点P到直线l的距离的最大值;
(2)若曲线C上所有的点均在直线l的右下方,求a的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,已知底角为![]() 的等腰梯形
的等腰梯形![]() ,底边
,底边![]() 长为7
长为7![]() ,腰长为
,腰长为![]() ,当一条垂直于底边
,当一条垂直于底边![]() 垂足为
垂足为![]() 的直线
的直线![]() 由
由![]() 从左至右向
从左至右向![]() 移动(与梯形
移动(与梯形![]() 有公共点)时,直线
有公共点)时,直线![]() 把梯形分成两部分,令
把梯形分成两部分,令![]()
![]() ,记左边部分的面积为
,记左边部分的面积为![]() .
.

(1)试求![]() 1,
1,![]() 3时的
3时的![]() 值;
值;
(2)写出![]() 关于
关于![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼吸酒精含量阀值与检验》国家标准,新标准规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升,小于80毫克/百毫克升为饮酒驾车,血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车,经过反复试验,喝1瓶啤酒后酒精在人体血液中的变化规律的“散点图”如下:
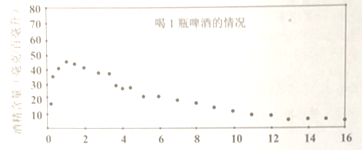
该函数模型如下:
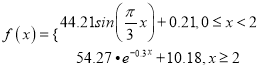
根据上述条件,回答以下问题:
(1)试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时后才可以驾车?(时间以整小时计算)
(参数数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x![]() ,g(x)=(4﹣lnx)lnx+b(b∈R).
,g(x)=(4﹣lnx)lnx+b(b∈R).
(1)若f(x)>0,求实数x的取值范围;
(2)若存在x1,x2∈[1,+∞),使得f(x1)=g(x2),求实数b的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com