
【题目】在如图所示的几何体中,![]() 平面
平面![]() .
.
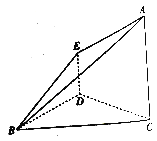
(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:(1)在![]() 中,由勾股定理可得
中,由勾股定理可得![]() .又
.又![]() 平面
平面![]() ,据此可得
,据此可得![]() .利用线面垂直的判断定理可得
.利用线面垂直的判断定理可得![]() 平面
平面![]() .
.
(2)(方法一)延长![]() ,
,![]() 相交于
相交于![]() ,连接
,连接![]() ,由题意可知二面角
,由题意可知二面角![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成二面角.取
所成二面角.取![]() 的中点为
的中点为![]() ,则
,则![]() 就是二面角
就是二面角![]() 的平面角.结合几何关系计算可得
的平面角.结合几何关系计算可得![]() .
.
(方法二)建立空间直角坐标系![]() ,计算可得平面
,计算可得平面![]() 的法向量
的法向量![]() .取平面
.取平面![]() 的法向量为
的法向量为![]() .利用空间向量计算可得
.利用空间向量计算可得![]() .
.
详解:(1)在![]() 中,
中,![]() .
.
所以![]() ,所以
,所以![]() 为直角三角形,
为直角三角形,![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
而![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)(方法一)如图延长![]() ,
,![]() 相交于
相交于![]() ,连接
,连接![]() ,
,
则平面![]() 平面
平面![]() .
.
二面角![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成二面角.
所成二面角.
因为![]() ,所以
,所以![]() 是
是![]() 的中位线.
的中位线.
![]() ,这样
,这样![]() 是等边三角形.
是等边三角形.
取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,因为
,因为![]() 平面
平面![]() .
.
所以![]() 就是二面角
就是二面角![]() 的平面角.
的平面角.
在![]() ,所以
,所以![]() .
.

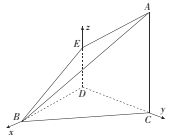
(方法二)建立如图所示的空间直角坐标系![]() ,可得
,可得![]() .
.
![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则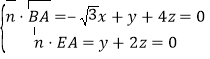
令![]() 得
得![]() .
.
取平面![]() 的法向量为
的法向量为![]() .
.
设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,
,
则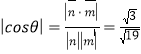 ,从而
,从而![]() .
.


科目:高中数学 来源: 题型:
【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最大值为60°.
其中正确的是________.(填写所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x),g(x)分别由下表给出,


则f[g(1)]的值为________,满足f[g(x)]>g[f(x)]的x的值是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族![]() 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当![]() 中
中![]() (
(![]() )的成员自驾时,自驾群体的人均通勤时间为
)的成员自驾时,自驾群体的人均通勤时间为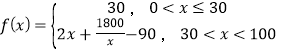 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为
影响,恒为![]() 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族![]() 的人均通勤时间
的人均通勤时间![]() 的表达式;讨论
的表达式;讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散.分析结果和实验表明,用![]() 表示学生掌握和接收概念的能力(
表示学生掌握和接收概念的能力(![]() 的值越大,表示接受能力越强),
的值越大,表示接受能力越强),![]() 表示提出和讲授概念的时间(单位:分钟),可以有以下公式:
表示提出和讲授概念的时间(单位:分钟),可以有以下公式: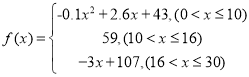
(1)开讲多少分钟后,学生的接受能力最强?能维持多长时间?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,线段
上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 作不与
作不与![]() 轴重合的直线
轴重合的直线![]() ,设
,设![]() 与圆
与圆![]() 相交于
相交于![]() 两点,与椭圆相交于
两点,与椭圆相交于![]() 两点,当
两点,当![]() 且
且![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com