
【题目】已知直线l1过点A(﹣1,0),且斜率为k,直线l2过点B(1,0),且斜率为﹣2k,其中k≠0,又直线l1与l2交于点M.
(1)求动点M的轨迹方程;
(2)若过点N( ![]() ,1)的直线l交动点M的轨迹于C、D两点,且N为线段CD的中点,求直线l的方程.
,1)的直线l交动点M的轨迹于C、D两点,且N为线段CD的中点,求直线l的方程.
【答案】
(1)解:设M(x,y),
∵直线l1与l2交于点M,
∴联立得: 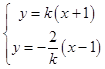 (k≠0),
(k≠0),
消去k得: ![]() =﹣2,
=﹣2,
则动点M的轨迹方程为2x2+y2=2(x≠±1)
(2)解:由(1)得M的轨迹方程为2x2+y2=2(x≠±1),
设点C(x1,y1),D(x2,y2),则有2x12+y12=2①,2x22+y22=2②,
①﹣②得:2(x1﹣x2)(x1+x2)+(y1﹣y2)(y1+y2)=0,即 ![]() =﹣2×
=﹣2× ![]() ,
,
∵N( ![]() ,1)为CD的中点,
,1)为CD的中点,
∴x1+x2=1,y1+y2=2,
∴直线l的斜率k=﹣1,
∴直线l的方程为y﹣1=﹣(x﹣ ![]() ),即2x+2y﹣3=0
),即2x+2y﹣3=0
【解析】(1)设M坐标为(x,y),表示出两直线方程,联立消去k即可确定出M的轨迹方程;(2)设出C与D坐标,分别代入M的轨迹方程,整理由根据N为CD中点,求出直线l斜率,即可确定出直线l方程.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 命题“![]() ”的否定是“
”的否定是“![]() ”
”
B. “![]() 在
在![]() 上恒成立”
上恒成立”![]() “
“![]() 在
在![]() 上恒成立”
上恒成立”
C. 命题“已知![]() ,若
,若![]() ,则
,则![]() 或
或![]() ”是真命题
”是真命题
D. 命题“若![]() ,则函数
,则函数![]() 只有一个零点”的逆命题为真命题
只有一个零点”的逆命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a(2cos2 ![]() +sinx)+b
+sinx)+b
(1)若a=﹣1,求f(x)的单调增区间;
(2)若x∈[0,π]时,f(x)的值域是[5,8],求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣ax﹣1.
(1)若f(x)在(﹣∞,+∞)上单调递增,求实数a的取值范围;
(2)是否存在实数a,使f(x)在(﹣1,1)上单调递减?若存在,求出a的取值范围;若不存在试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次抗洪抢险中,准备用射击的方法引爆从桥上游漂流而下的一个巨大的汽油灌,已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆.每次射击相互独立,且命中概率都是![]() ,求(1)油罐被引爆的概率;(2)如果引爆或子弹打光则停止射击,设射击次数为
,求(1)油罐被引爆的概率;(2)如果引爆或子弹打光则停止射击,设射击次数为![]() ,求
,求![]() 的分布列.
的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com