
 中,
中, 平面
平面 ,底面
,底面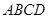 是平行四边形,
是平行四边形, ,
,
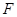 是
是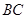 的中点
的中点
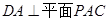
 上确定一点
上确定一点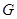 ,使
,使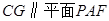 ,求三棱锥
,求三棱锥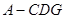 的体积.
的体积.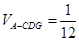 .
.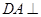 平面
平面 ,先证明线线垂直,即证
,先证明线线垂直,即证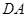 垂直平面
垂直平面 内的两条相交直线即可,由题意
内的两条相交直线即可,由题意 平面
平面 ,即
,即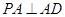 ,在平面
,在平面 内再找一条垂线即可,由已知
内再找一条垂线即可,由已知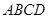 是平行四边形,
是平行四边形, ,从而可得
,从而可得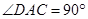 ,即
,即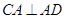 ,从而可证
,从而可证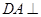 平面
平面 ;(Ⅱ)试在线段
;(Ⅱ)试在线段 上确定一点
上确定一点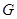 ,使
,使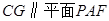 ,求三棱锥
,求三棱锥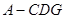 的体积,注意到
的体积,注意到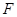 是
是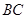 的中点,可取
的中点,可取 的中点为
的中点为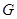 ,在平面
,在平面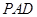 内作
内作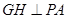 于
于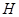 ,则四边形
,则四边形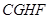 为平行四边形,
为平行四边形, 的中点
的中点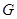 即为所确定的点,求三棱锥
即为所确定的点,求三棱锥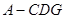 的体积,可转化为求三棱锥
的体积,可转化为求三棱锥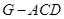 的体积,由题意容易求得,从而得解.
的体积,由题意容易求得,从而得解.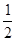 AD. (8分)
AD. (8分)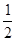 PA=
PA=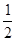
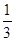 S△ACD·GS=
S△ACD·GS=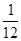 . (12分)
. (12分)

 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:不详 题型:单选题
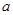 升水.平放在地面,则水面正好过圆锥的顶点
升水.平放在地面,则水面正好过圆锥的顶点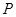 ,若将容器倒置如图2,水面也恰过点
,若将容器倒置如图2,水面也恰过点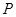 .以下命题正确的是( ).
.以下命题正确的是( ).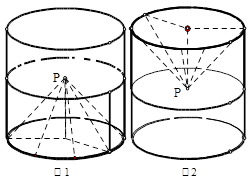
A.圆锥的高等于圆柱高的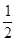 ; ; |
B.圆锥的高等于圆柱高的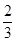 ; ; |
C.将容器一条母线贴地,水面也恰过点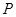 ; ; |
D.将容器任意摆放,当水面静止时都过点 . . |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com