
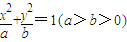 过点
过点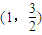 ,且离心率为
,且离心率为 ,A、B是椭圆上纵坐标不为零的两点,若
,A、B是椭圆上纵坐标不为零的两点,若 ,且
,且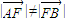 ,其中F为椭圆的左焦点.
,其中F为椭圆的左焦点. ,所以
,所以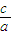 =
= ,因为椭圆过(1,
,因为椭圆过(1, ),所以把(1,
),所以把(1, )代入椭圆方程成立,再根据a,b,c的关系式,就可解出a,b的值,求出椭圆的方程.
)代入椭圆方程成立,再根据a,b,c的关系式,就可解出a,b的值,求出椭圆的方程.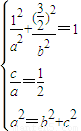 ,解得a2=4,b2=3
,解得a2=4,b2=3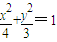
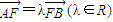
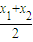 =
=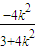 ,y=k(x+1)=
,y=k(x+1)=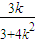
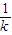 (x-x)
(x-x)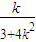 =-
=-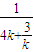
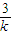 |≥4
|≥4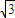 ,当且仅当|k|=
,当且仅当|k|=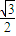 时取“=“
时取“=“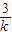 ≥4
≥4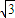 或4k+
或4k+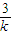 ≤-4
≤-4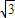
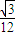 ,0]∪(0,
,0]∪(0,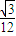 ].
].

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
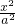 +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).查看答案和解析>>
科目:高中数学 来源:2012年安徽省淮北市高考数学二模试卷(文科)(解析版) 题型:解答题
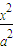 +
+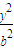 =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).查看答案和解析>>
科目:高中数学 来源:2012年安徽省淮南市高考数学二模试卷(理科)(解析版) 题型:解答题
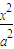 +
+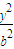 =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).查看答案和解析>>
科目:高中数学 来源:2012年安徽省淮北市高考数学二模试卷(理科)(解析版) 题型:解答题
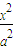 +
+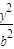 =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com