
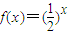 ,数列{an} 满足
,数列{an} 满足 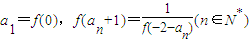
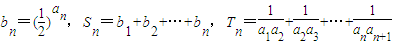 ,求 Sn与 Tn.
,求 Sn与 Tn. ,得出
,得出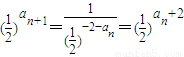 ,进而得出an+1-an=2,从而确定数列{an} 是首项为1,公差为2的等差数列,即可求出通项公式;
,进而得出an+1-an=2,从而确定数列{an} 是首项为1,公差为2的等差数列,即可求出通项公式; ,公比为
,公比为 的等比数列,然后根据等比数列的前n项和求出 Sn,再根据裂项的方法求出Tn.
的等比数列,然后根据等比数列的前n项和求出 Sn,再根据裂项的方法求出Tn.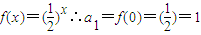
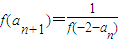
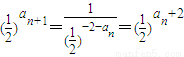
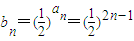

 ,公比为
,公比为 的等比数列
的等比数列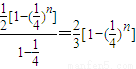
 +
+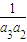 +…+
+…+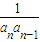 =
= +
+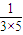 +…+
+…+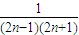 =
= [(1-
[(1- )+
)+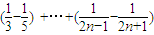 ]=
]=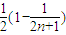 (13分)
(13分)

科目:高中数学 来源:2009-2010学年广东省湛江市遂溪一中高三(下)4月月考数学试卷(理科)(解析版) 题型:解答题
 ,数列{an}满足
,数列{an}满足
 ,试比较 Sn与
,试比较 Sn与 的大小,并加以证明.
的大小,并加以证明.查看答案和解析>>
科目:高中数学 来源:2010年北京市昌平区高考数学二模试卷(理科)(解析版) 题型:解答题
 ,数列{an}满足
,数列{an}满足 .
. ,这些项能够构成以a1为首项,q(0<q<5,q∈N*)为公比的等比数列
,这些项能够构成以a1为首项,q(0<q<5,q∈N*)为公比的等比数列 ,k∈N*.若存在,写出nk关于k的表达式;若不存在,说明理由.
,k∈N*.若存在,写出nk关于k的表达式;若不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com