
【题目】已知三棱锥P﹣ABC中,AC⊥BC,AC=BC=2,PA=PB=PC=3,O是AB中点,E是PB中点.
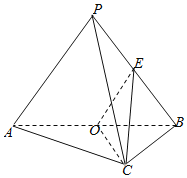
(1)证明:平面PAB⊥平面ABC;
(2)求点B到平面OEC的距离.
【答案】(1)见解析(2)![]()
【解析】
(1)连结PO,利用等腰三角形的性质证得![]() ,利用勾股定理计算证明证得
,利用勾股定理计算证明证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,进而证得平面
,进而证得平面![]() 平面
平面![]() .
.
(2)利用等体积法,由![]() 列方程,解方程求得
列方程,解方程求得![]() 到平面
到平面![]() 的距离.
的距离.
(1)连结PO,在△PAB中,PA=PB,O是AB中点,
∴PO⊥AB,
又∵AC=BC=2,AC⊥BC,∴![]() .
.
∵PA=PB=3,∴![]() ,PC2=PO2+OC2,
,PC2=PO2+OC2,
∴PO⊥OC.
又AB∩OC=O,AB平面ABC,OC平面ABC,
∴PO⊥平面ABC,
∵PO平面PAB,∴平面PAB⊥平面ABC.
(2)∵OE是△PAB的中位线,∴![]() .
.
∵O是AB中点,AC=BC,∴OC⊥AB.
又平面PAB⊥平面ABC,两平面的交线为AB,∴OC⊥平面PAB,
∵OE平面PAB,∴OC⊥OE.
设点B到平面OEC的距离为d,则VB﹣OEC=VE﹣OBC,
∴![]() ,
,
∴点B到平面OEC的距离:
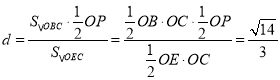 .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】(本小题14分)设![]() ,
, ![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)如果存在![]() ,使得
,使得![]() 成立,
成立,
求满足上述条件的最大整数![]() ;
;
(3)如果对任意的![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2x的焦点为F,过焦点F的直线交抛物线于A,B两点,过A,B作准线的垂线交准线与P,Q两点.R是PQ的中点.
(1)证明:以PQ为直径的圆恒过定点F.
(2)证明:AR∥FQ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为圆心的圆与直线:
为圆心的圆与直线:![]() 相切.
相切.
(1)求圆![]() 的方程;
的方程;
(2)若圆![]() 上有两点
上有两点![]() 关于直线
关于直线![]() 对称,且
对称,且![]() ,求直线MN的方程;
,求直线MN的方程;
(3)圆![]() 与x轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求
与x轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某商品在过去的100天内的销售量(单位:件)和价格(单位:元)均为时间![]() (单位:天)的函数,且销售量满足
(单位:天)的函数,且销售量满足![]() =
=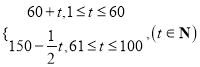 ,价格满足
,价格满足![]() =
=![]() .
.
(1)求该种商品的日销售额![]() 与时间
与时间![]() 的函数关系;
的函数关系;
(2)若销售额超过16610元,商家认为该商品的收益达到理想程度,请判断该商品在哪几天的收益达到理想程度?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装店对过去100天实体店和网店的销售量(单位:件)进行了统计,制成频率分布直方图如下:
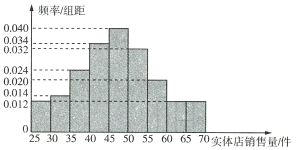
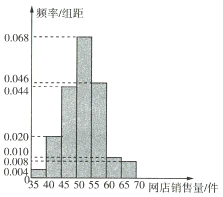
(1)已知该服装店过去100天的销售中,实体店和网店的销售量都不低于50件的频率为0.24,求过去100天的销售中,实体店和网店至少有一边销售量不低于50件的天数;
(2)根据频率分布直方图,求该服装店网店销售量的中位数的估计值(精确到0.01).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,点
,点![]() 在直线上,过点
在直线上,过点![]() 作圆
作圆![]() 的切线
的切线![]() ,切点为
,切点为![]() .
.
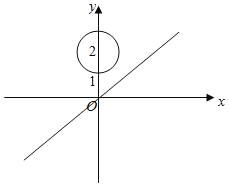
(1)若过点![]() 的坐标为
的坐标为![]() ,求切线
,求切线![]() 方程;
方程;
(2)求四边形![]() 面积的最小值;
面积的最小值;
(3)求证:经过![]() 三点的圆必过定点,并求出所有定点坐标.
三点的圆必过定点,并求出所有定点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com