
【题目】已知椭圆C:![]() 上顶点为A,右顶点为B,离心率
上顶点为A,右顶点为B,离心率![]() ,O为坐标原点,原点到直线AB的距离为
,O为坐标原点,原点到直线AB的距离为![]() .
.
(1)求椭圆C的标准方程;
(2)直线![]() 与椭圆C相交于E、F两不同点,若椭圆C上一点P满足
与椭圆C相交于E、F两不同点,若椭圆C上一点P满足![]() .求△EPF面积的最大值及此时的
.求△EPF面积的最大值及此时的![]() .
.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 的面积的最大值为
的面积的最大值为![]() .
.
【解析】
(1)设出直线![]() 的方程为::
的方程为::![]() ,原点到直线
,原点到直线![]() 的距离为
的距离为![]() ,列出关系式, 通过
,列出关系式, 通过![]() ,利用离心率,求出
,利用离心率,求出![]() ,
,![]() ,得到椭圆
,得到椭圆![]() 的标准方程.
的标准方程.
(2)联立直线与椭圆方程, 设![]() ,
,![]() ,
,![]() ,
,![]() ,利用韦达定理, 以及弦长公式, 点到直线的距离,
,利用韦达定理, 以及弦长公式, 点到直线的距离,![]() ,利用二次函数的最值, 求解
,利用二次函数的最值, 求解![]() 的面积的最大值,以及
的面积的最大值,以及![]() 的值
的值
(1)由题意,![]() ,则
,则![]() ,①
,①
∵A(0,b),B(a,0),则直线AB的方程为:![]() ,即为
,即为![]() ,
,
∵原点到直线AB的距离为![]() ,
,
∴![]() ,
,
∴![]() ,②
,②
∵![]() ,③
,③
由①②③得:![]() ,
,
所以椭圆C的标准方程为:![]() ;
;
(2)由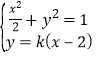 可得:
可得:![]() ,
,
设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
∴![]()
又点O到直线EF的距离![]() ,
,
∵![]() ,
,
∴
又因为![]() ,又
,又![]() ,∴
,∴![]() ,
,
令![]() ,则,
,则,
![]()
所以当![]() 时,最大值为:
时,最大值为:![]()
所以当![]() 时,△EPF的面积的最大值为
时,△EPF的面积的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,AB=AD,BD⊥CD,点E、F分别是棱BC、BD的中点.
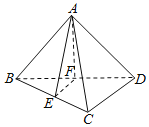
(1)求证:EF∥平面ACD;
(2)求证:AE⊥BD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,五面体A﹣BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A﹣BC﹣C1为直二面角.
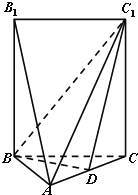
(1)D在AC上运动,当D在何处时,有AB1//平面BDC1,并且说明理由;
(2)当AB1//平面BDC1时,求二面角C﹣BC1﹣D余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为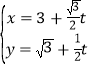 (
(![]() 为参数),点
为参数),点![]() 的极坐标为
的极坐标为![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在底面是菱形的四棱锥![]() 中,
中,![]() ,点E在PD上,且
,点E在PD上,且![]() .
.

(1)证明:![]() 平面ABCD;
平面ABCD;
(2)求二面角![]() 的大小;
的大小;
(3)棱PC上是否存在一点F,使![]() 平面AEC?证明你的结论.
平面AEC?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1且an﹣an﹣1=3×(![]() )n﹣2(n≥2,n∈N*).
)n﹣2(n≥2,n∈N*).
(1)求数列{an}的通项公式:
(2)若对任意的n∈N*,不等式1≤man≤5恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,两焦点与短轴的一个端点的连线构成的三角形面积为
,两焦点与短轴的一个端点的连线构成的三角形面积为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设与圆O:![]() 相切的直线l交椭圆C于A,B两点(O为坐标原点),求△AOB面积的最大值。
相切的直线l交椭圆C于A,B两点(O为坐标原点),求△AOB面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在十九大“建设美丽中国”的号召下,某省级生态农业示范县大力实施绿色生产方案,对某种农产品的生产方式分别进行了甲、乙两种方案的改良。为了检查甲、乙两种方案的改良效果,随机在这两种方案中各任意抽取了40件产品作为样本逐件称出它们的重量(单位:克),重量值落在![]() 之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
产品重量 | 甲方案频数 | 乙方案频数 |
| 6 | 2 |
| 8 | 12 |
| 14 | 18 |
| 8 | 6 |
| 4 | 2 |
(1)根据上表数据求甲(同组中的重量值用组中点数值代替)方案样本中40件产品的平均数和中位数
(2)由以上统计数据完成下面![]() 列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
甲方案 | 乙方案 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
参考公式:![]() ,其中
,其中![]() .
.
临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.814 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com