
ЁОЬтФПЁПьГВЈРЦѕЪ§СаЃЌжИЕФЪЧетбљвЛИіЪ§СаЃК1ЃЌ1ЃЌ2ЃЌ3ЃЌ5ЃЌ8ЃЌ13ЃЌ21ЃЌЁЃЌдкЪ§бЇЩЯЃЌьГВЈРЦѕЪ§Са{an}ЖЈвхШчЯТЃКa1ЃНa2ЃН1ЃЌanЃНanЉ1+anЉ2ЃЈnЁн3ЃЌnЁЪNЃЉЃЌЫцзХnЕФдіДѓЃЌ![]() дНРДдНБЦНќЛЦН№ЗжИю
дНРДдНБЦНќЛЦН№ЗжИю![]() 0.618ЃЌЙЪДЫЪ§СавВГЦЛЦН№ЗжИюЪ§СаЃЌЖјвдan+1ЁЂanЮЊГЄКЭПэЕФГЄЗНаЮГЦЮЊЁАзюУРГЄЗНаЮЁБЃЌвбжЊФГЁАзюУРГЄЗНаЮЁБЕФУцЛ§дМЮЊ200ЦНЗНРхУзЃЌдђИУГЄЗНаЮЕФГЄДѓдМЪЧЃЈ ЃЉ
0.618ЃЌЙЪДЫЪ§СавВГЦЛЦН№ЗжИюЪ§СаЃЌЖјвдan+1ЁЂanЮЊГЄКЭПэЕФГЄЗНаЮГЦЮЊЁАзюУРГЄЗНаЮЁБЃЌвбжЊФГЁАзюУРГЄЗНаЮЁБЕФУцЛ§дМЮЊ200ЦНЗНРхУзЃЌдђИУГЄЗНаЮЕФГЄДѓдМЪЧЃЈ ЃЉ
A.20РхУзB.19РхУзC.18РхУзD.17РхУз
 вЛОэИуЖЈЯЕСаД№АИ
вЛОэИуЖЈЯЕСаД№АИ УћаЃзївЕБОЯЕСаД№АИ
УћаЃзївЕБОЯЕСаД№АИ ЧсЧЩЖсЙкжмВтдТПМжБЭЈУћаЃЯЕСаД№АИ
ЧсЧЩЖсЙкжмВтдТПМжБЭЈУћаЃЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіЖрУцЬхЕФжБЙлЭММАШ§ЪгЭМШчЭМЫљЪОЃЌЦфжаM ЃЌN ЗжБ№ЪЧAFЁЂBC ЕФжаЕу
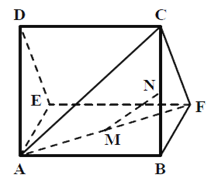
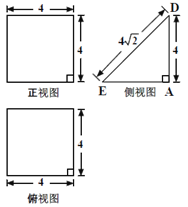
ЃЈ1ЃЉЧѓжЄЃКMNЁЮЦНУцCDEFЃЛ
ЃЈ2ЃЉЧѓЖрУцЬхA-CDEFЕФЬхЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШ§РтзЖ![]() жаЃЌ
жаЃЌ![]() ЃЌЁї
ЃЌЁї![]() ЮЊЕШБпШ§НЧаЮЃЌЖўУцНЧ
ЮЊЕШБпШ§НЧаЮЃЌЖўУцНЧ![]() ЕФгрЯвжЕЮЊ
ЕФгрЯвжЕЮЊ![]() ЃЌЕБШ§РтзЖЕФЬхЛ§зюДѓЪБЃЌЦфЭтНгЧђЕФБэУцЛ§ЮЊ
ЃЌЕБШ§РтзЖЕФЬхЛ§зюДѓЪБЃЌЦфЭтНгЧђЕФБэУцЛ§ЮЊ![]() .дђШ§РтзЖЬхЛ§ЕФзюДѓжЕЮЊЃЈ ЃЉ
.дђШ§РтзЖЬхЛ§ЕФзюДѓжЕЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИїЯюЮЊе§Ъ§ЕФЪ§Са![]() ШчЙћТњзуЃКДцдкЪЕЪ§
ШчЙћТњзуЃКДцдкЪЕЪ§![]() ЃЌЖдШЮвте§ећЪ§nЃЌ
ЃЌЖдШЮвте§ећЪ§nЃЌ![]() КуГЩСЂЃЌЧвДцдке§ећЪ§nЃЌЪЙЕУ
КуГЩСЂЃЌЧвДцдке§ећЪ§nЃЌЪЙЕУ![]() Лђ
Лђ![]() ГЩСЂЃЌдђГЦЪ§Са
ГЩСЂЃЌдђГЦЪ§Са![]() ЮЊЁАНєУмЪ§СаЁБЃЌkГЦЮЊЁАНєУмЪ§СаЁБ
ЮЊЁАНєУмЪ§СаЁБЃЌkГЦЮЊЁАНєУмЪ§СаЁБ![]() ЕФЁАНєУмЖШЁБЃЎвбжЊЪ§Са
ЕФЁАНєУмЖШЁБЃЎвбжЊЪ§Са![]() ЕФИїЯюЮЊе§Ъ§ЃЌЧАnЯюКЭЮЊ
ЕФИїЯюЮЊе§Ъ§ЃЌЧАnЯюКЭЮЊ![]() ЃЌЧвЖдШЮвте§ећЪ§nЃЌ
ЃЌЧвЖдШЮвте§ећЪ§nЃЌ![]() ЃЈAЃЌBЃЌCЮЊГЃЪ§ЃЉКуГЩСЂЃЎ
ЃЈAЃЌBЃЌCЮЊГЃЪ§ЃЉКуГЩСЂЃЎ
ЃЈ1ЃЉЕБ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪБЃЌ
ЪБЃЌ
ЂйЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
ЂкжЄУїЪ§Са![]() ЪЧЁАНєУмЖШЁБЮЊ3ЕФЁАНєУмЪ§СаЁБЃЛ
ЪЧЁАНєУмЖШЁБЮЊ3ЕФЁАНєУмЪ§СаЁБЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌвбжЊЪ§Са
ЪБЃЌвбжЊЪ§Са![]() КЭЪ§Са
КЭЪ§Са![]() ЖМЮЊЁАНєУмЪ§СаЁБЃЌЁАНєУмЖШЁБЗжБ№ЮЊ
ЖМЮЊЁАНєУмЪ§СаЁБЃЌЁАНєУмЖШЁБЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌЧѓЪЕЪ§BЕФШЁжЕЗЖЮЇЃЎ
ЃЌЧѓЪЕЪ§BЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§![]() ЕФЖЈвхгђЮЊ
ЕФЖЈвхгђЮЊ![]() ЃЌВЂТњзувдЯТЬѕМўЃКЂйЖдШЮвт
ЃЌВЂТњзувдЯТЬѕМўЃКЂйЖдШЮвт![]() ЃЌга
ЃЌга![]() ЃЛЂкЖдШЮвт
ЃЛЂкЖдШЮвт![]() ЃЌга
ЃЌга![]() ЃЛЂл
ЃЛЂл![]() .
.
ЃЈЂёЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈЂђЃЉЧѓжЄЃК![]() дк
дк![]() ЩЯЪЧЕЅЕїдіКЏЪ§ЃЛ
ЩЯЪЧЕЅЕїдіКЏЪ§ЃЛ
ЃЈЂѓЃЉШє![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВOЃКx2+y2ЃН3ЃЌжБЯпPAгыдВOЯрЧагкЕуAЃЌжБЯпPBДЙжБyжсгкЕуBЃЌЧв|PB|ЃН2|PA|.
ЃЈ1ЃЉЧѓЕуPЕФЙьМЃEЕФЗНГЬЃЛ
ЃЈ2ЃЉЙ§ЕуЃЈ1ЃЌ0ЃЉЧвгыxжсВЛжиКЯЕФжБЯпгыЙьМЃEЯрНЛгкPЃЌQСНЕуЃЌдкxжсЩЯЪЧЗёДцдкЖЈЕуDЃЌЪЙЕУxжсЪЧЁЯPDQЕФНЧЦНЗжЯпЃЌШєДцдкЃЌЧѓГіDЕузјБъЃЌШєВЛДцдкЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌ
ЃЌ![]()
ЃЈ1ЃЉЧѓ![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() дкЦфЙЋЙВЕу
дкЦфЙЋЙВЕу![]() ДІЧаЯпЯрЭЌЃЌЧѓЪЕЪ§aЕФжЕЃЛ
ДІЧаЯпЯрЭЌЃЌЧѓЪЕЪ§aЕФжЕЃЛ
ЃЈ3ЃЉМЧ![]() ЃЌШєКЏЪ§
ЃЌШєКЏЪ§![]() ДцдкСНИіСуЕуЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇ.
ДцдкСНИіСуЕуЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпlЕФВЮЪ§ЗНГЬ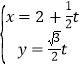 (tЮЊВЮЪ§)ЃЌвдзјБъдЕуЮЊМЋЕуЃЌxжсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯпCЕФМЋзјБъЗНГЬЮЊЃК
(tЮЊВЮЪ§)ЃЌвдзјБъдЕуЮЊМЋЕуЃЌxжсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯпCЕФМЋзјБъЗНГЬЮЊЃК![]() ЃЎ
ЃЎ
![]() Ђё
Ђё![]() жБЯпlЕФВЮЪ§ЗНГЬЛЏЮЊМЋзјБъЗНГЬЃЛ
жБЯпlЕФВЮЪ§ЗНГЬЛЏЮЊМЋзјБъЗНГЬЃЛ
![]() Ђђ
Ђђ![]() ЧѓжБЯпlгыЧњЯпCНЛЕуЕФМЋзјБъ
ЧѓжБЯпlгыЧњЯпCНЛЕуЕФМЋзјБъ![]() Цфжа
Цфжа![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЖўЯюЪН![]() ЕФеЙПЊЪНжаЃЌЧАШ§ЯюЯЕЪ§ЕФОјЖджЕГЩЕШВюЪ§СаЁЃ
ЕФеЙПЊЪНжаЃЌЧАШ§ЯюЯЕЪ§ЕФОјЖджЕГЩЕШВюЪ§СаЁЃ
ЃЈ1ЃЉЧѓеЙПЊЪНЕФЕкЫФЯюЃЛ
ЃЈ2ЃЉЧѓеЙПЊЪНЕФГЃЪ§ЯюЃЛ
ЃЈ3ЃЉЧѓеЙПЊЪНжаИїЯюЕФЯЕЪ§КЭЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com