练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在等差数列{an}中，Sn表示前n项和，a2+a8=18-a5，则S9=________．

    54
    分析：根据给出的数列是等差数列，由等差中项的概念结合a2+a8=18-a5求a5，然后再由等差数列的前n项和公式写出S9，把出S9可转化为9a5，则结论可求．
    解答：因为数列{an}是等差数列，所以a5是a2与a8的等差中项，所以a2+a8=2a5，
    由a2+a8=18-a5，所以2a5=18-a5，所以，a5=6．
    在等差数列{an}中，．
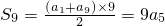
    所以，S9=9×6=54．
    故答案为54．
    点评：本题考查了等差数列的前n项和，考查了等差中项的概念，有穷等差数列如果含有奇数项，则其前n项和为n倍的中间项，此题是基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在等差数列{an}中，a1=-2010，其前n项的和为Sn．若
    S2010
    2010
    -
    S2008
    2008
    =2，则S2010=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，a1+3a8+a15=60，则2a9-a10的值为
    12
    12
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知在等差数列{an}中，d＞0，a2008、a2009是方程x2-3x-5=0的两个根，那么使得前n项和Sn为负值的最大的n的值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，已知a1=2，a2+a3=13，则a4+a5+a6等于=
    42
    42
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，若S4=1，S8=4，则a17+a18+a19+a20的值=
    9
    9
    ．

    查看答案和解析>>

    同步练习册答案