
| A. | -8058 | B. | 8058 | C. | -8060 | D. | 8060 |
分析 观察到自变量前后对称相加和为定值2,故令a=1,x1+x2=2,求得f(x1)+f(x2)=-4,从而求得要求式子的值.
解答 解:观察到自变量前后对称相加和为定值2,故令a=1,∵x1+x2=2,
∴$f({x_1})+f({x_2})={x_1}^3-3{x_1}^2-sin(π{x_1})+{(2-{x_1})^3}-3{(2-{x_1})^2}-sin[π(2-{x_1})]=-4$,为定值,
∴$S=f(\frac{4029}{2015})+f(\frac{4028}{2015})+…+f(\frac{2}{2015})+f(\frac{1}{2015})$,
故2S=-4×4029,∴S=-8058.
故选:A.
点评 本题主要考查正弦函数的函数的图象的对称性,求函数的值,属于中档题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:选择题
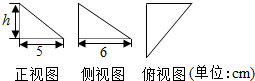
| A. | 25xcm2 | B. | $\frac{77π}{2}$cm2 | C. | 77πcm2 | D. | 144πcm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ③④ | C. | ②⑤ | D. | ②③⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
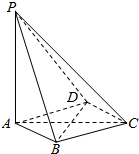 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com