练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下面几种推理是合情推理的是 （ ）

    ①由圆的性质类比出球的有关性质

    ②由直角三角形、等腰三角形、等边三角形内角和是180°归纳出所有三角形的内角和都是180°

    ③某次考试张军成绩是100分，由此推出全班同学成绩都是100分

    ④数列1，0，1，0，…，推测出每项公式

    A. ①② B. ①③④ C. ①②④ D. ②④

    【答案】C

    【解析】①为类比推理,在推理过程中由圆的性质类比出有关球的有关性质; ②为归纳推理, 由直角三角形、等腰三角形、等边三角形内角和是180°归纳出所有三角形的内角和都是180,符合归纳推理的定义,即由特殊到一般的推理过程; ③不是合情推理,是由个别到全体的推理过程; ④为归纳推理,由数列的前四项归纳猜想数列的通项公式;综上可知选C.

    点睛:合情推理分为归纳推理和类比推理,都是根据已有的事实,经过观察,分析,比较,联想,再进行归纳,类比,然后提出猜想的推理.归纳推理由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,是由部分到整体,由个别到一般的推理;类比推理由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理,是由特殊到特殊的推理.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在五棱锥中，平面平面，且．

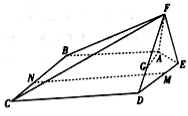
    （1）已知点在线段上，确定的位置，使得平面；

    （2）点分别在线段上，若沿直线将四边形向上翻折，与恰好重合，求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆，直线经过点A (1，0).

    （1）若直线与圆C相切，求直线的方程；

    （2）若直线与圆C相交于P，Q两点，求三角形CPQ面积的最大值，并求此时直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法错误的是（ ）

    A. 在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高

    B. 在线性回归分析中，回归直线不一定过样本点的中心

    C. 在回归分析中， 为0.98的模型比为0.80的模型拟合的效果好

    D. 自变量取值一定时，因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在透明塑料制成的长方体容器内灌进一些水（未满），现将容器底面一边固定在底面上，再将容器倾斜，随着倾斜度的不同，有下列四种说法：

    ①水的部分始终呈棱柱状；

    ②水面四边形的面积为定值；

    ③棱始终与水面平行；

    ④若， ，则是定值.

    则其中正确命题的个数的是（ ）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一项针对人们休闲方式的调查结果如下：受调查对象总计124人，其中女性70人，男性54人.女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动.

    （1）根据以上数据建立一个的列联表；

    （2）根据下列提供的独立检验临界值表，你最多能有多少把握认为性别与休闲方式有关系？

    独立检验临界值表：

    0.50

    0.40

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    0.455

    0.708

    1.323

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    参考公式： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

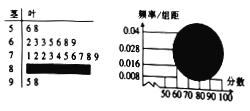
    【题目】如图，某校高一（1）班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分，据此解答如下问题：

    （1）求该班全体男生的人数及分数在之间的男生人数；

    （2）根据频率分布直方图，估计该班全体男生的数学平均成绩（同一组中的数据用该组区间的中点值代表）；

    （3）从分数在中抽取两个男生，求抽取的两男生分别来自、的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】经测算，某型号汽车在匀速行驶过程中每小时耗油量 (升)与速度 (千米／每小时) 的关系可近似表示为：.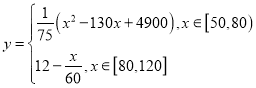

    （Ⅰ）该型号汽车速度为多少时，可使得每小时耗油量最低？

    （Ⅱ）已知两地相距120公里，假定该型号汽车匀速从地驶向地，则汽车速度为多少时总耗油量最少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学从高三男生中随机抽取100名学生，将他们的身高数据进行整理，得到下侧的频率分布表

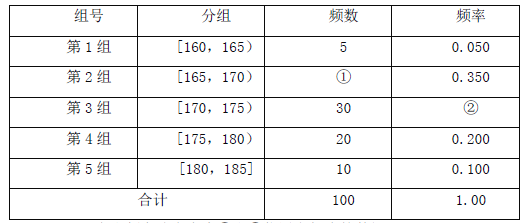
    （Ⅰ）求出频率分布表中①和②位置上相应的数据；

    （Ⅱ）为了能对学生的体能做进一步了解，该校决定在第3，4，5 组中用分层抽样的方法抽取6 名学生进行体能测试，求第3，4，5 组每组各应抽取多少名学生进行测试；

    （Ⅲ）在（Ⅱ）的前提下，学校决定在6 名学生中随机抽取2 名学生进行引体向上测试，求第4 组中至少有一名学生被抽中的概率.

    查看答案和解析>>

    同步练习册答案