Question

16．设定义在R上的函数f（x）=$\left\{\begin{array}{l}{2（x=0）}\\{lo{g}_{3}|x|（x≠0）}\end{array}\right.$，若关于x的方程f²（x）+bf（x）+c=0恰有3个不同的实数解，则bc=（　　）

• A． -9
• B． 9
• C． -16
• D． 16

Answer 1

分析 设t=f（x），作出函数f（x）的图象，根据关于x的方程f²（x）+bf（x）+c=0恰有3个不同的实数解x₁，x₂，x₃，得到t的取值情况即可求出结论．

解答 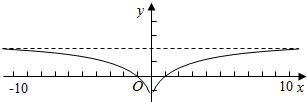解：设t=f（x），
则关于x的方程f²（x）+bf（x）+c=0
等价为t²+bt+c=0，
作出f（x）的图象如图：
由图象可知当t=2时，方程f（x）=2有三个根，
当t≠2时方程f（x）=t有两个不同的实根，
∴若若关于x的方程f²（x）+bf（x）+c=0恰有3个不同的实数解x₁，x₂，x₃，
则等价为t²+bt+c=0只有一个根t=2，
由f（x）=2得，x=0，或者log₃|x|=2，
即得x=±9，
即三个根x₁，x₂，x₃，分别为0，9或-9，
由韦达定理可得2+2=-b，2×2=c，
即b=-4，c=4，可得bc=-16．
故选：C．

点评 本题主要考查方程根的个数的应用，利用换元法将方程转化为二次方程，根据二次方程根的分布是解决本题的关键，利用数形结合是解决本题的基本思想．