
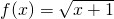 属于MD,求k的取值范围;
属于MD,求k的取值范围;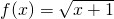 在[0,+∞)为增函数
在[0,+∞)为增函数 =
=
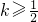 ,此即为所求.
,此即为所求. ,
, ,
, ,
, 中另有一根,矛盾.
中另有一根,矛盾.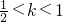 ,
, =sin2kπ-ksin2π<0,
=sin2kπ-ksin2π<0, 中另有一根,矛盾.∴
中另有一根,矛盾.∴ .
. 符合题意.
符合题意. 时,由y=sinx图象在连接两点(0,0),(x,sinx)的线段的上方知sinkx>ksinx
时,由y=sinx图象在连接两点(0,0),(x,sinx)的线段的上方知sinkx>ksinx 时,
时, .
. 时,sinkx>0,sinx<0,∴h(x)>0.
时,sinkx>0,sinx<0,∴h(x)>0. 满足题意.
满足题意. 为所求.
为所求. 进行整理,根据其取值范围即可得到k的取值范围;
进行整理,根据其取值范围即可得到k的取值范围;

 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:单选题
 已知集合M={x||x-7|<9},N={x|y=
已知集合M={x||x-7|<9},N={x|y= },且M,N都是全集U的子集,则下图韦恩图中阴影部分表示的集合
},且M,N都是全集U的子集,则下图韦恩图中阴影部分表示的集合查看答案和解析>>
科目:高中数学 来源: 题型:单选题


查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 恒成立,设a=f(-
恒成立,设a=f(- ),b=f(2),c=f(3),则a,b,c的大小关系为
),b=f(2),c=f(3),则a,b,c的大小关系为查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com