
【题目】酒后违法驾驶机动车危害巨大,假设驾驶人员血液中的酒精含量为![]() (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当![]() 时,为酒后驾车;当
时,为酒后驾车;当![]() 时,为醉酒驾车.如图为某市交管部分在一次夜间行动中依法查出的
时,为醉酒驾车.如图为某市交管部分在一次夜间行动中依法查出的![]() 名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中
名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中![]() 人数包含
人数包含![]() ).
).
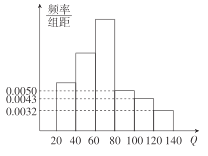
(Ⅰ)求查获的醉酒驾车的人数;
(Ⅱ)从违法驾车的![]() 人中按酒后驾车和醉酒驾车利用分层抽样抽取
人中按酒后驾车和醉酒驾车利用分层抽样抽取![]() 人做样本进行研究,再从抽取的
人做样本进行研究,再从抽取的![]() 人中任取
人中任取![]() 人,求
人,求![]() 人中含有醉酒驾车人数
人中含有醉酒驾车人数![]() 的分布列和数学期望.
的分布列和数学期望.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间与极值;
的单调区间与极值;
(2)当![]() 时,令
时,令![]() ,若
,若![]() 在
在![]() 上有两个零点,求实数
上有两个零点,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图像上所有点都在不等式组
的图像上所有点都在不等式组![]() 所表示的平面区域内,求实数a的取值范围.
所表示的平面区域内,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品在近30天内每件的销售价格P(元)与时间t(天)的函数是:P=![]()
该商品的日销售量Q(件)与时间t(天)的函数关系是:Q=﹣t+40(0<t≤30,t∈N*),求这种商品的日销售金额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+ax(a∈R).
(1)当a=3时,求函数f(x)在[![]() ,2]上的最大值和最小值;
,2]上的最大值和最小值;
(2)当函数f(x)在(![]() ,2)单调时,求a的取值范围.
,2)单调时,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体ABCD﹣A1B1C1D1中,点M,N分别在线段AB1、BC1上,且AM=BN.以下结论:①AA1⊥MN;②A1C1∥MN;③MN∥平面A1B1C1D1;④MN与A1C1异面,⑤MN与 A1C1成30°.其中有可能成立的结论的个数为( ) 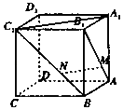
A.5
B.4
C.3
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com