
【题目】一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表:
温度x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵个数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
(I)根据散点图判断,![]() 与
与![]() 哪一个适宜作为产卵数
哪一个适宜作为产卵数![]() 关于温度
关于温度![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(II)根据(I)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)红铃虫是棉区危害较重的害虫,可从农业、物理和化学三个方面进行防治,其中农业方面防治有3种方法,物理方面防治有1种方法,化学方面防治3种方法,现从7种方法中选3种方法进行综合防治(即3种方法不能全部来自同一方面,至少来自两个方面),X表示在综合防治中农业方面的防治方法的种数,求X的分布列及数学期望E(X).
附:可能用到的公式及数据表中(表中![]() ,
,![]() =
=![]()
![]() ,
,![]() =
=![]()
![]() ,
,![]() =
=![]()
![]() )
)
|
|
|
|
|
|
|
27.430 | 3.612 | 81.290 | 147.700 | 2763.764 | 705.592 | 40.180 |
对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]()

【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】
(I)由散点图可以判断,![]() 适宜作为作为产卵数y关于温度x的回归方程类型. (II)令
适宜作为作为产卵数y关于温度x的回归方程类型. (II)令![]() ,先建立w关于x的线性回归方程式,再建立y关于x的回归方程.(Ⅲ)依题意得随机变量X=0,1,2,再分别求它们对应的概率,即得X的分布列和期望.
,先建立w关于x的线性回归方程式,再建立y关于x的回归方程.(Ⅲ)依题意得随机变量X=0,1,2,再分别求它们对应的概率,即得X的分布列和期望.
(I)由散点图可以判断,![]() 适宜作为作为产卵数y关于温度x的回归方程类型。
适宜作为作为产卵数y关于温度x的回归方程类型。
(II)令![]() ,先建立w关于x的线性回归方程式,由数据得
,先建立w关于x的线性回归方程式,由数据得
![]() ,
,![]()
 ,
,
所以w关于x的线性回归方程为![]() ,
,
因此y关于x的回归方程为![]()
(Ⅲ)依题意得随机变量X=0,1,2,基本事件总数为![]()
当X=0时,选用物理方法1种、化学方法3选2,共有![]() ,
,![]()
当X=1时, ![]()
当X=2时,![]()
所以X的分布列
X | 0 | 1 | 2 |
P |
|
|
|
数学期望E(X) ![]()


科目:高中数学 来源: 题型:
【题目】![]() ,
,![]() 两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
![]() 组:10,11,12,13,14,15,16
组:10,11,12,13,14,15,16
![]() 组:12,13,15,16,17,14,
组:12,13,15,16,17,14,![]()
假设所有病人的康复时间互相独立,从![]() ,
,![]() 两组随机各选1人,
两组随机各选1人,![]() 组选出的人记为甲,
组选出的人记为甲,![]() 组选出的
组选出的
人记为乙.
(Ⅰ)求甲的康复时间不少于14天的概率;
(Ⅱ)如果![]() ,求甲的康复时间比乙的康复时间长的概率;
,求甲的康复时间比乙的康复时间长的概率;
(Ⅲ)当![]() 为何值时,
为何值时,![]() ,
,![]() 两组病人康复时间的方差相等?(结论不要求证明)
两组病人康复时间的方差相等?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“五四青年节”到来之际,启东中学将开展一系列的读书教育活动.为了解高二学生读书教育情况,决定采用分层抽样的方法从高二年级![]() 四个社团中随机抽取12名学生参加问卷调査.已知各社团人数统计如下:
四个社团中随机抽取12名学生参加问卷调査.已知各社团人数统计如下:
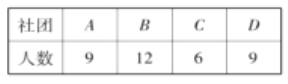
(1)若从参加问卷调查的12名学生中随机抽取2名,求这2名学生来自同一个社团的概率;
(2)在参加问卷调查的12名学生中,从来自![]() 三个社团的学生中随机抽取3名,用
三个社团的学生中随机抽取3名,用![]() 表示从
表示从![]() 社团抽得学生的人数,求
社团抽得学生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和
项和![]() ,
,
(1)求数列![]() 的通项公式;
的通项公式;
(2)令![]() ,记数列
,记数列![]() 前n项和为
前n项和为![]() ,求
,求![]() ;
;
(3)利用第二问结果,设![]() 是整数,问是否存在正整数n,使等式
是整数,问是否存在正整数n,使等式![]() 成立?若存在,求出
成立?若存在,求出![]() 和相应的
和相应的![]() 值;若不存在,说明理由.
值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 与
与![]() 的交点,
的交点, ![]() 为棱
为棱![]() 上一点.
上一点.
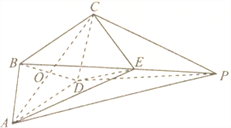
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,三棱锥
,三棱锥![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E、F分别是PC、AD中点,
(1)求证:DE//平面PFB;
(2)求PB与面PCD所成角的正切值。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是___(请填写所有正确的命题序号).
①命题“若![]() ,则
,则![]() ”的否命题为:“若
”的否命题为:“若![]() ,则
,则![]() ”;
”;
②命题“若![]() ,则
,则![]() ”的逆否命题为真命题;
”的逆否命题为真命题;
③条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
④已知![]() 时,
时,![]() ,若
,若![]() 是锐角三角形,则
是锐角三角形,则![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com