
【题目】某个年级有男生560人,女生420人,用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本,则此样本中男生人数为 .
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,某市准备在道路EF的一侧修建一条运动比赛道,赛道的前一部分为曲线段FBC,该曲线段是函数 ![]() (A>0,ω>0),x∈[﹣4,0]时的图象,且图象的最高点为B(﹣1,2).赛道的中间部分为长
(A>0,ω>0),x∈[﹣4,0]时的图象,且图象的最高点为B(﹣1,2).赛道的中间部分为长 ![]() 千米的直线跑道CD,且CD∥EF.赛道的后一部分是以O为圆心的一段圆弧
千米的直线跑道CD,且CD∥EF.赛道的后一部分是以O为圆心的一段圆弧 ![]() .
. 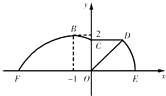
(1)求ω的值和∠DOE的大小;
(2)若要在圆弧赛道所对应的扇形ODE区域内建一个“矩形草坪”,矩形的一边在道路EF上,一个顶点在半径OD上,另外一个顶点P在圆弧 ![]() 上,且∠POE=θ,求当“矩形草坪”的面积取最大值时θ的值.
上,且∠POE=θ,求当“矩形草坪”的面积取最大值时θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,
, ![]() .
.
(1)当n=1,2,3时,分别比较f(n)与g(n)的大小(直接给出结论);
(2)由(1)猜想f(n)与g(n)的大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为正数的等差数列,其前
是公差为正数的等差数列,其前![]() 项和为
项和为![]() ,且
,且![]() ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 满足
满足![]() ,
, ![]() .①求数列
.①求数列![]() 的通项公式;②是否存在正整数
的通项公式;②是否存在正整数![]() ,
, ![]() (
(![]() ),使得
),使得![]() ,
, ![]() ,
, ![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() ,
, ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ax2+(a﹣2)x﹣2(a∈R).
(1)解关于x的不等式f(x)≥0;
(2)若a>0,当﹣1≤x≤1时,f(x)≤0时恒成立,求a的取值范围.
(3)若当﹣1<a<1时,f(x)>0时恒成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2sin4x+2cos4x+cos22x﹣3.
(1)求函数f(x)的最小正周期.
(2)求函数f(x)在闭区间[ ![]() ]上的最小值并求当f(x)取最小值时,x的取值集合.
]上的最小值并求当f(x)取最小值时,x的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=4sin(2x ![]() )(x∈R),有下列命题: ①y=f(x)的表达式可改写为y=4cos(2x﹣
)(x∈R),有下列命题: ①y=f(x)的表达式可改写为y=4cos(2x﹣ ![]() );
);
②y=f(x)是以2π为最小正周期的周期函数;
③y=f(x)的图象关于点 ![]() 对称;
对称;
④y=f(x)的图象关于直线x=﹣ ![]() 对称.
对称.
其中正确的命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
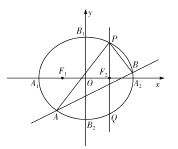
【题目】如图,已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,两个焦点分别为
,两个焦点分别为![]() ,
, ![]() ,四边形
,四边形![]() 的面积是四边形
的面积是四边形![]() 的面积的2倍.
的面积的2倍.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右焦点且垂直于
的右焦点且垂直于![]() 轴的直线交椭圆
轴的直线交椭圆![]() 于
于![]() 两点,
两点, ![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的两点.若直线
两侧的两点.若直线![]() 过点
过点![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com