
【题目】在平面直角坐标系![]() 中,动点P到两点
中,动点P到两点![]() 、
、![]() 的距离之差的绝对值等于
的距离之差的绝对值等于![]() .设点P的轨迹为C.
.设点P的轨迹为C.
(1)求C的轨迹方程;
(2)过点![]() 的直线l与曲线C交于M,N两点,且Q恰好为线段
的直线l与曲线C交于M,N两点,且Q恰好为线段![]() 的中点,求直线l的方程.
的中点,求直线l的方程.
【答案】(1)![]() (2)
(2)![]() .
.
【解析】
(1)根据条件,结合双曲线定义即可求得双曲线的标准方程.
(2)当斜率不存在时,不符合题意;当斜率存在时,设出直线方程,联立双曲线,变形后由中点坐标公式可求得斜率,即可求得直线方程.
(1)动点P到两点![]() 的距离之差的绝对值等于
的距离之差的绝对值等于![]() ,且
,且![]() ,
,
设![]() ,则
,则![]() ,
,
根据双曲线定义可知动点P的轨迹C为双曲线,
焦点在![]() 轴上,且
轴上,且![]() ,所以
,所以![]() ,
,
则双曲线的标准方程为C:![]() .
.
(2)过点![]() 的直线l与曲线C交于M,N两点,且Q恰好为线段
的直线l与曲线C交于M,N两点,且Q恰好为线段![]() 的中点,
的中点,
当直线斜率不存在时,直线方程为![]() ,则由双曲线对称性可知线段
,则由双曲线对称性可知线段![]() 的中点在
的中点在![]() 轴上,所以不满足题意;
轴上,所以不满足题意;
当斜率存在时,设直线方程为![]() ,设
,设![]() ,
,
则 ,化简可得
,化简可得![]() ,
,
因为有两个交点,所以![]()
化简可得![]() 恒成立,
恒成立,
所以 ,
,
因为![]() 恰好为线段
恰好为线段![]() 的中点,则
的中点,则 ,
,
化简可得![]() ,
,
所以直线方程为![]() ,即
,即![]() .
.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某高校大一新生中,来自东部地区的学生有2400人、中部地区学生有1600人、西部地区学生有1000人.从中选取100人作样本调研饮食习惯,为保证调研结果相对准确,下列判断正确的有( )
①用分层抽样的方法分别抽取东部地区学生48人、中部地区学生32人、西部地区学生20人;
②用简单随机抽样的方法从新生中选出100人;
③西部地区学生小刘被选中的概率为![]() ;
;
④中部地区学生小张被选中的概率为![]()
A. ①④ B. ①③ C. ②④ D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面ABCD,底部ABCD为菱形,E为CD的中点.
平面ABCD,底部ABCD为菱形,E为CD的中点.

(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;
(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 关于直线
关于直线![]() 对称的点Q在椭圆上,则椭圆的离心率为______;若过
对称的点Q在椭圆上,则椭圆的离心率为______;若过![]() 且斜率为
且斜率为![]() 的直线与椭圆相交于AB两点,且
的直线与椭圆相交于AB两点,且![]() ,则
,则![]() ___.
___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有250人参与学习先修课程.
(Ⅰ)这两年学校共培养出优等生150人,根据下图等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过0.01的前提下认为学习先修课程与优等生有关系?

优等生 | 非优等生 | 总计 | |
学习大学先修课程 | 250 | ||
没有学习大学先修课程 | |||
总计 | 150 |
(Ⅱ)某班有5名优等生,其中有2名参加了大学生先修课程的学习,在这5名优等生中任选3人进行测试,求这3人中至少有1名参加了大学先修课程学习的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
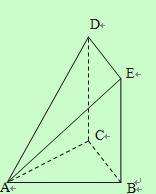
【题目】某设计部门承接一产品包装盒的设计(如图所示),客户除了要求![]() 、
、![]() 边的长分别为
边的长分别为![]() 和
和![]() 外,还特别要求包装盒必需满足:①平面
外,还特别要求包装盒必需满足:①平面![]() 平面
平面![]() ;②平面
;②平面![]() 与平面
与平面![]() 所成的二面角不小于
所成的二面角不小于![]() ;③包装盒的体积尽可能大.
;③包装盒的体积尽可能大.
若设计部门设计出的样品满足:![]() 与
与![]() 均为直角且
均为直角且![]() 长
长![]() ,矩形
,矩形![]() 的一边长为
的一边长为![]() ,请你判断该包装盒的设计是否能符合客户的要求?说明理由.
,请你判断该包装盒的设计是否能符合客户的要求?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com