Question

【题目】某大型单位举行了一次全体员工都参加的考试，从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数（以十位数字为茎，个位数字为叶）：

若分数不低于95分，则称该员工的成绩为“优秀”.

（1）从这20人中任取3人，求恰有1人成绩“优秀”的概率；

（2）根据这20人的分数补全下方的频率分布表和频率分布直方图，并根据频率分布直方图解决下面的问题.

组别	分组	频数	频率
1
2
3
4

①估计所有员工的平均分数（同一组中的数据用该组区间的中点值作代表）；

②若从所有员工中任选3人，记表示抽到的员工成绩为“优秀”的人数，求的分布列和数学期望.

Answer 1

【答案】（1）；（2）①82，②分布列见解析，

【解析】

（1）从20人中任取3人共有种结果，恰有1人成绩“优秀”共有种结果，利用古典概型的概率计算公式计算即可；

（2）①平均数的估计值为各小矩形的组中值与其面积乘积的和；②要注意服从的是二项分布，不是超几何分布，利用二项分布的分布列及期望公式求解即可.

（1）设从20人中任取3人恰有1人成绩“优秀”为事件，

则，所以，恰有1人“优秀”的概率为.

（2）

组别	分组	频数	频率
1		2		0.01
2		6		0.03
3		8		0.04
4		4		0.02

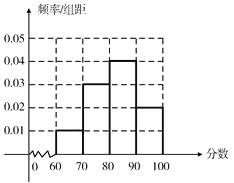
①，

估计所有员工的平均分为82

②的可能取值为0、1、2、3，随机选取1人是“优秀”的概率为，

∴；

；

；

；

∴的分布列为

	0	1	2	3

∵，∴数学期望.