
| A�� | ��t��-2ʱ������g��x�����ĸ���� | B�� | ��t=-2ʱ������g��x����������� | ||
| C�� | ��t=$\frac{1}{4}$ʱ������g��x����һ����� | D�� | ��-2��t��$\frac{1}{4}$ʱ������g��x����������� |
���� ��������f��x����ͼ����m=f��x�����ɵ�m��1ʱ��m=f��x����������m��1ʱ��m=f��x����һ�������ݶ��κ�����ͼ������ʷ���tȡ��ֵͬʱ��g��x��=m2+m+t���ĸ���������������ۺ����ۿɵã�
��� �⣺����f��x��=$\left\{\begin{array}{l}{{3}^{x}\\;��x��0��}\\{lo{g}_{3}��-x��\\;��x��0��}\end{array}\right.$��ͼ����ͼ��ʾ��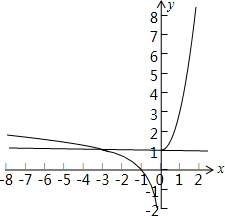
��m=f��x����m��1ʱ��m=f��x����������m��1ʱ��m=f��x����һ����
��t��-2����g��x��=m2+m+t=0����������һ������1��һ��С��1
��ʱ��g��x��=0������������A����
��t=-2����g��x��=f2��x��+f��x��-2=��m+2����m-1��=0
��ʱm=-2��m=1����ʱg��x��=0����������
��g��x����������㣬��B��ȷ��
��t=$\frac{1}{4}$����g��x��=f2��x��+f��x��+$\frac{1}{4}$=��m+$\frac{1}{2}$��2=0
��ʱm=-$\frac{1}{2}$������ͼ�ɵã���ʱ����m=0��һ������
��g��x����һ����㣬��C��ȷ��
��-2��t��$\frac{1}{4}$����g��x��=m2+m+t=0����������������1
��ʱ��g��x��=0������������D��ȷ��
��ѡ��A
���� ���⿼����Ĵ����Լ����ĸ����жϣ������ν�ϲ��������ն��κ�����ͼ��������ǽ��Ĺؼ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{4}$ | B�� | -$\frac{3}{4}$ | C�� | $\frac{\sqrt{3}}{2}$ | D�� | -$\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 6 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com