
【题目】由小到大排列的一组数据x1 , x2 , x3 , x4 , x5 , 其中每个数据都小于﹣1,则样本1,x1 , ﹣x2 , x3 , ﹣x4 , x5的中位数为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:因为x1<x2<x3<x4<x5<﹣1,题目中数据共有六个,排序后为x1<x3<x5<1<﹣x4<﹣x2 ,
故中位数是按从小到大排列后第三,第四两个数的平均数作为中位数,
故这组数据的中位数是 ![]() (x5+1).
(x5+1).
故选:C.
【考点精析】掌握平均数、中位数、众数是解答本题的根本,需要知道⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两位同学在5次考试中的数学成绩用茎叶图表示如图,中间一列的数字表示数学成绩的十位数字,两边的数字表示数学成绩的个位数字,若甲、乙两人的平均成绩分别是 ![]() ,
, ![]() ,则下列说法正确的是( )
,则下列说法正确的是( ) 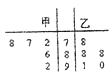
A.![]() ,甲比乙成绩稳定
,甲比乙成绩稳定
B.![]() ,乙比甲成绩稳定
,乙比甲成绩稳定
C.![]() ,甲比乙成绩稳定
,甲比乙成绩稳定
D.![]() ,乙比甲成绩稳定
,乙比甲成绩稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为C的圆经过O(0,0))和A(4,0)两点,线段OA的垂直平分线和圆C交于M,N两点,且|MN|=2 ![]()
(1)求圆C的方程
(2)设点P在圆C上,试问使△POA的面积等于2的点P共有几个?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
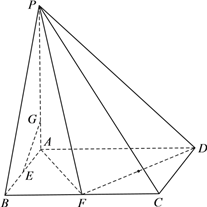
【题目】如图,四棱锥P-ABCD中,底面ABCD是矩形,PA![]() 面ABCD,且AB=2,AD=4,
面ABCD,且AB=2,AD=4,
AP=4,F是线段BC的中点.
⑴ 求证:面PAF![]() 面PDF;
面PDF;
⑵ 若E是线段AB的中点,在线段AP上是否存在一点G,使得EG![]() 面PDF?若存在,求出线段AG的长度;若不存在,说明理由.
面PDF?若存在,求出线段AG的长度;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F分别为AD,A1B1的中点.
(1)求证:DB1⊥CD1;
(2)求三棱锥B﹣EFC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在[0,1]上的函数f(x)满足:①f(0)=0;②f(x)+f(1﹣x)=1;③f( ![]() )=
)= ![]() f(x);④当0≤x1<x2≤1时,f(x1)≤f(x2).则f(
f(x);④当0≤x1<x2≤1时,f(x1)≤f(x2).则f( ![]() )= .
)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
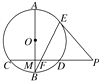
【题目】如图,已知⊙O中,直径AB垂直于弦CD,垂足为M,P是CD延长线上一点,PE切⊙O于点E,连接BE交CD于点F,证明:
(1)∠BFM=∠PEF;
(2)PF2=PD·PC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布图如图所示,下表是年龄的频率分布表.
,得到的频率分布图如图所示,下表是年龄的频率分布表.
![]()

(1)现要从年龄较小的第![]() 组中用分层抽样的方法抽取6人,则年龄第
组中用分层抽样的方法抽取6人,则年龄第![]() 组人数分别是多少?
组人数分别是多少?
(2)在(1)的条件下,从这6中随机抽取2参加社区宣传交流活动,X表示第3组中抽取的人数,求X的分布列和期望值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com