练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，角A、B、C所对的边分别是a、b、c.
    （1）在△ABC中，A=60º，B=75º，c=20，求边a的长；
    （2）若△ABC的面积，求∠C的度数.

    （1）（2）

    解析试题分析：（1）先求角，在用正弦定理求边。（2）根据余弦定理可得，可计算得的正切值，即可求得。
    试题解析：（1）依题意,                            （2分）
    由正弦定理得，                      （3分）
    即                        （6分）
    （2）由，得.       （9分）
    ∴，因为，所以.         （12分）
    考点：1正弦定理；2余弦定理。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    如图，渔船甲位于岛屿A的南偏西60°方向的B处，且与岛屿A相距12海里，渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行，若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙，刚好用2h追上，此时到达C处．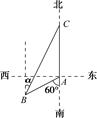

    (1)求渔船甲的速度；
    (2)求sinα的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为30°,已知摄影爱好者的身高约为米(将眼睛S距地面的距离SA按米处理).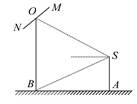

    (1)求摄影爱好者到立柱的水平距离AB和立柱的高度OB.
    (2)立柱的顶端有一长为2米的彩杆MN,且MN绕其中点O在摄影爱好者与立柱所在的平面内旋转.在彩杆转动的任意时刻,摄影爱好者观察彩杆MN的视角∠MSN(设为θ)是否存在最大值?若存在,请求出∠MSN取最大值时cosθ的值;若不存在,请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某旅游景点有一处山峰，游客需从景点入口A处向下沿坡角为α的一条小路行进a百米后到达山脚B处，然后沿坡角为β的山路向上行进b百米后到达山腰C处，这时回头望向景点入口A处俯角为θ，由于山势变陡到达山峰D坡角为γ，然后继续向上行进c百米终于到达山峰D处，游览风景后，此游客打算乘坐由山峰D直达入口A的缆车下山结束行程，如图所示，假设A，B，C，D四个点在同一竖直平面．
     
    (1)求B，D两点的海拔落差h；
    (2)求AD的长

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在△ABC中，角A，B，C对应的边分别是 a，b，c.已知cos 2A－3cos(B＋C)＝1.
    (1)求角A的大小；
    (2)若△ABC的面积S＝5，b＝5，求sin Bsin C的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在中，角所对的边分别为，且，.
    （1）求的值；
    （2）若，，求三角形ABC的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在中,三个内角所对边的长分别为,已知.
    （Ⅰ）判断的形状;
    （Ⅱ）设向量,若,求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知向量m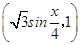＝，n＝.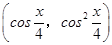
    (1)若m·n＝1，求cos 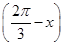的值；
    (2)记f(x)＝m·n，在△ABC中，角A，B，C的对边分别是a，b，c，且满足(2a－c)cos B＝bcos C，求函数f(A)的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在△ABC中，角A，B，C的对边分别为a，b，c，且2cos2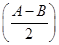cos B－sin(A－B)sin B＋cos(A＋C)＝－.
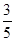    (1)求cos A的值；
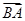    (2)若a＝4，b＝5，求向量在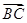方向上的投影．

    查看答案和解析>>

    同步练习册答案