【答案】
分析:(Ⅰ)由题意知定义域D=(-m,+∞),由f(x)=x-ln(x+m),x∈(-m,+∞),知
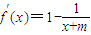
=
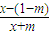
,由此能求出当m≤1时,f(x)≥0.
(Ⅱ)当m>1时,f(1-m)=1-m<0,故函数f(x)=x-ln(x+m)在(-m,-m+1]上为减函数,由m>1知-m+e
-m∈(-m,-m+1],f(-m+e
-m)=-m+e
-m-ln(-m+e
-m+m)=e
-m>0,知函数f(x)在(e
-m-m,1-m)内有唯一零点,从而可知函数f(x)在(-m,-m+1]内有唯一零点,由此入手能够证明对任意的m∈(1,+∞),方程f(x)=0在D内有且只有两个实数根.
解答:解:(Ⅰ)由题意知定义域D=(-m,+∞),∵f(x)=x-ln(x+m),x∈(-m,+∞),
∴
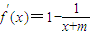
=
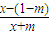
,
令f′(x)=0,得x=1-m.
当x∈(-m,1-m)时,f′(x)<0,f(x)为减函数,f(x)>f(1-m);
当x∈(1-m,+∞)时,f′(x)>0,f(x)为增函数,f(x)>f(1-m);
故函数f(x)在定义域D内的最小值为f(1-m)=1-m,即f(x)≥f(1-m)=1-m,
故当m≤1时,f(x)≥0.
(Ⅱ)证明:由(Ⅰ)知,当m>1时,f(1-m)=1-m<0,
函数f(x)=x-ln(x+m)在(-m,-m+1]上为减函数,
又由m>1知-m+e
-m∈(-m,-m+1],
且由f(-m+e
-m)=-m+e
-m-ln(-m+e
-m+m)=e
-m>0,
知函数f(x)在(e
-m-m,1-m)内有唯一零点,
从而可知函数f(x)在(-m,-m+1]内有唯一零点,
令g(x)=e
2x-3x(x>1),
则g′(x)=2e
2x-3,
当x>1时,g′(x)=2e
2x-3>2e
2-3>0,
故函数g(x)在区间(1,+∞)上递增.
于是,g(x)>g(1)=e
2-3>0,
从而可知,当m>1时,
f(e
2m-m)=e
2m-3m>0.
函数f(x)=x-ln(x+m)在(-m+1,-m+e
2m]上递增,
∵m>1,∴-m+e
2m∈(-m+1,-m+e
2m],
且由f(-m+e
2m)=-m+e
2m-ln(-m+e
2m+m)=e
2m-3m>0,
知函数f(x)在(-m+1,-m+e
2m]内有唯一零点,
从而可知函数f(x)在(-m+1,+∞)内有唯一零点.
综上所述,对任意的m∈(1,+∞),方程f(x)=0在D内有且只有两个实数根.
点评:本题考查函数与方程的综合应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

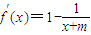 =
=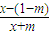 ,由此能求出当m≤1时,f(x)≥0.
,由此能求出当m≤1时,f(x)≥0.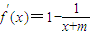 =
=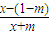 ,
,

 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案