
| 1 | 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 17 |
| 8 |
| 1 |
| 2 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 17 |
| 8 |
| 1 |
| 2 |


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
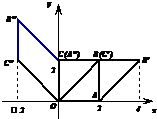 (Ⅰ)如图,正方形OABC在二阶矩阵M对应的切变变换作用下变为平行四边形OA′B′C′,平行四边形OA'B'C'在二阶矩阵N对应的旋转变换作用下变为平行四边形OA''B''C'',求将正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵.
(Ⅰ)如图,正方形OABC在二阶矩阵M对应的切变变换作用下变为平行四边形OA′B′C′,平行四边形OA'B'C'在二阶矩阵N对应的旋转变换作用下变为平行四边形OA''B''C'',求将正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵.
|
| π |
| 4 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年潍坊市四模文) 直线l∶y=ax+1与双曲线C∶![]() 相交于A,B两点.
相交于A,B两点.
(1)a为何值时,以AB为直径的圆过原点;
(2)是否存在这样的实数a,使A,B关于直线x-2y=0对称,若存在,求a的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第64课时):第八章 圆锥曲线方程-直线与圆锥的位置关系(1)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com