
ЁОЬтФПЁПФГаЃЮЊСЫСЫНтИпвЛаТЩњЪЧЗёдИвтВЮМгОќбЕЃЌЫцЛњЕїВщСЫ80УћаТЩњЃЌЕУЕНШчЯТ2ЁС2СаСЊБэ
дИвт | ВЛдИвт | КЯМЦ | |
Фа | x | 5 | M |
ХЎ | y | z | 40 |
КЯМЦ | N | 25 | 80 |
ЃЈ1ЃЉаДГіБэжаxЃЌyЃЌzЃЌMЃЌNЕФжЕЃЌВЂХаЖЯЪЧЗёга99.9%ЕФАбЮеШЯЮЊдИвтВЮМгОќбЕгыадБ№гаЙиЃЛ
ЃЈ2ЃЉдкБЛЕїВщЕФВЛдИвтВЮМгОќбЕЕФбЇЩњжаЃЌЫцЛњГщГі3ШЫЃЌМЧет3ШЫжаФаЩњЕФШЫЪ§ЮЊІЮЃЌЧѓІЮЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ВЮПМЙЋЪНЃК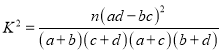
ИНЃК
PЃЈK2Ёнk0ЃЉ | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ЁОД№АИЁП(1)MЃН40ЃЌxЃН35ЃЌzЃН20ЃЌyЃН20ЃЌNЃН55ЃЌга99.9%ЕФАбЮеШЯЮЊдИвтВЮМгжОдИепЬюБЈХрбЕгыадБ№гаЙиЃЎ(2)ЗжВМСаМћЯъНтЃЌE(ІЮЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнБэИёжаЪ§ОнЃЌМДПЩЧѓЕУxЃЌyЃЌzЃЌMЃЌNЕФжЕЃЌдйМЦЫу![]() ЃЌНсКЯВЮПМБэИёМДПЩзїГіХаЖЯЃЛ
ЃЌНсКЯВЮПМБэИёМДПЩзїГіХаЖЯЃЛ
ЃЈ2ЃЉСаГіІЮЕФШЁжЕЃЌИљОнЙХЕфИХаЭИХТЪМЦЫуЙЋЪНЧѓЕУЗжВМСаЃЌдйИљОнЗжВМСаМЦЫуЪ§бЇЦкЭћМДПЩ.
ЃЈ1ЃЉгЩБэИёЪ§ОнПЩжЊЃК
MЃН80Љ40ЃН40ЃЌ
xЃН40Љ5ЃН35ЃЌ
zЃН25Љ5ЃН20ЃЌ
yЃН40Љ20ЃН20ЃЌ
NЃН80Љ25ЃН55ЃЌ
ЁпK2![]() 13.09ЃО10.828ЃЌ
13.09ЃО10.828ЃЌ
Ёрга99.9%ЕФАбЮеШЯЮЊдИвтВЮМгжОдИепЬюБЈХрбЕгыадБ№гаЙиЃЎ
ЃЈ2ЃЉдкБЛЕїВщЕФВЛдИвтВЮМгОќбЕЕФбЇЩњжаЃЌЫцЛњГщГі3ШЫЃЌ
МЧет3ШЫжаФаЩњЕФШЫЪ§ЮЊІЮЃЌдђІЮЕФПЩФмШЁжЕЮЊ0,1,2,3ЃЌ
PЃЈІЮЃН0ЃЉ![]() ЃЌ
ЃЌ
PЃЈІЮЃН1ЃЉ![]() ЃЌ
ЃЌ
PЃЈІЮЃН2ЃЉ![]() ЃЌ
ЃЌ
PЃЈІЮЃН3ЃЉ![]() ЃЌ
ЃЌ
ЁрІЮЕФЗжВМСаЮЊЃК
ІЮ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
EЃЈІЮЃЉ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жавбжЊЭждВ
жавбжЊЭждВ![]() Й§Еу
Й§Еу ЃЌЦфзѓЁЂгвНЙЕуЗжБ№ЮЊ
ЃЌЦфзѓЁЂгвНЙЕуЗжБ№ЮЊ![]() ЃЌРыаФТЪЮЊ
ЃЌРыаФТЪЮЊ![]() .
.
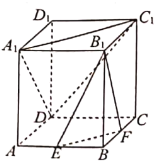
ЃЈ1ЃЉЧѓЭждВEЕФЗНГЬЃЛ
ЃЈ2ЃЉШєAЃЌBЗжБ№ЮЊЭждВEЕФзѓЁЂгвЖЅЕуЃЌЖЏЕуMТњзу![]() ЃЌЧвMAНЛЭждВEгкЕуP.
ЃЌЧвMAНЛЭждВEгкЕуP.
ЃЈiЃЉЧѓжЄЃК![]() ЮЊЖЈжЕЃЛ
ЮЊЖЈжЕЃЛ
ЃЈiiЃЉЩшPBгывдPMЮЊжБОЖЕФдВЕФСэвЛНЛЕуЮЊQЃЌЮЪЃКжБЯпMQЪЧЗёЙ§ЖЈЕуЃЌВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() .
.
ЃЈ1ЃЉШє![]() КуГЩСЂЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
КуГЩСЂЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєЙигкxЕФЗНГЬ![]() гаСНИіВЛЭЌЕФНтЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇ.
гаСНИіВЛЭЌЕФНтЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкКЏЪ§fЃЈxЃЉИјГіЖЈвхЃКЩшfЁфЃЈxЃЉЪЧКЏЪ§yЃНfЃЈxЃЉЕФЕМЪ§ЃЌfЁхЃЈxЃЉЪЧКЏЪ§fЁфЃЈxЃЉЕФЕМЪ§ЃЌШєЗНГЬfЁхЃЈxЃЉЃН0гаЪЕЪ§Нтx0ЃЌдђГЦЕуЃЈx0ЃЌfЃЈx0ЃЉЃЉЮЊКЏЪ§yЃНfЃЈxЃЉЕФЁАЙеЕуЁБЃЎФГЭЌбЇОЙ§ЬНОПЗЂЯжЃКШЮКЮвЛИіШ§ДЮКЏЪ§fЃЈxЃЉЃНax3+bx2+cx+dЃЈaЁй0ЃЉЖМгаЁАЙеЕуЁБЃЛШЮКЮвЛИіШ§ДЮКЏЪ§ЖМгаЖдГЦжааФЃЌЧвЁАЙеЕуЁБОЭЪЧЖдГЦжааФЃЎИјЖЈКЏЪ§![]() ЃЌЧыФуИљОнЩЯУцЬНОПНсЙћЃЌМЦЫуfЃЈ
ЃЌЧыФуИљОнЩЯУцЬНОПНсЙћЃЌМЦЫуfЃЈ![]() ЃЉ+fЃЈ
ЃЉ+fЃЈ![]() ЃЉ+fЃЈ
ЃЉ+fЃЈ![]() ЃЉ+ЁЁ+fЃЈ
ЃЉ+ЁЁ+fЃЈ![]() ЃЉЃН_____ЃЎ
ЃЉЃН_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌШєЗНГЬ
ЃЌШєЗНГЬ![]() гаЮхИіВЛЭЌЕФИљЃЌдђЪЕЪ§
гаЮхИіВЛЭЌЕФИљЃЌдђЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЮЊЃЈ ЃЉ
ЕФШЁжЕЗЖЮЇЮЊЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкГЄЗНЬх![]() жаЃЌЕзУц
жаЃЌЕзУц![]() ЪЧБпГЄЮЊ
ЪЧБпГЄЮЊ![]() ЕФе§ЗНаЮЃЌ
ЕФе§ЗНаЮЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕу.
ЕФжаЕу.
ЃЈ1ЃЉЧѓжЄЃК![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓЦНУц
ЃЌЧѓЦНУц![]() гыЦНУц
гыЦНУц![]() ЫљГЩЖўУцНЧЕФе§ЯвжЕ.
ЫљГЩЖўУцНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ![]() ЃЌgЃЈxЃЉ
ЃЌgЃЈxЃЉ![]() 1ЃЎ
1ЃЎ
ЃЈ1ЃЉШєfЃЈaЃЉЃН2ЃЌЧѓЪЕЪ§aЕФжЕЃЛ
ЃЈ2ЃЉХаЖЯfЃЈxЃЉЕФЕЅЕїадЃЌВЂжЄУїЃЛ
ЃЈ3ЃЉЩшКЏЪ§hЃЈxЃЉЃНgЃЈxЃЉ![]() ЃЈxЃО0ЃЉЃЌШєhЃЈ2tЃЉ+mhЃЈtЃЉ+4ЃО0ЖдШЮвтЕФе§ЪЕЪ§tКуГЩСЂЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЎ
ЃЈxЃО0ЃЉЃЌШєhЃЈ2tЃЉ+mhЃЈtЃЉ+4ЃО0ЖдШЮвтЕФе§ЪЕЪ§tКуГЩСЂЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЫФРтзЖPЉABCDжаЃЌЕзУцABCDЪЧБпГЄЮЊ4ЕФе§ЗНаЮЃЌЁїPADЪЧвЛИіе§Ш§НЧаЮЃЌШєЦНУцPADЁЭЦНУцABCDЃЌдђИУЫФРтзЖЕФЭтНгЧђЕФБэУцЛ§ЮЊ_____.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕ![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ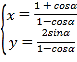 (
(![]() ЮЊВЮЪ§).вд
ЮЊВЮЪ§).вд![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌжБЯп
жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() (
(![]() )ЃЌНЋЧњЯп
)ЃЌНЋЧњЯп![]() ЯђзѓЦНвЦ2ИіЕЅЮЛГЄЖШЕУЕНЧњЯп
ЯђзѓЦНвЦ2ИіЕЅЮЛГЄЖШЕУЕНЧњЯп![]() .
.
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЦеЭЈЗНГЬКЭМЋзјБъЗНГЬЃЛ
ЕФЦеЭЈЗНГЬКЭМЋзјБъЗНГЬЃЛ
ЃЈ2ЃЉЩшжБЯп![]() гыЧњЯп
гыЧњЯп![]() НЛгк
НЛгк![]() СНЕуЃЌЧѓ
СНЕуЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com