
【题目】如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.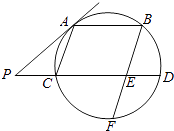
(1)求AC的长;
(2)试比较BE与EF的长度关系.
科目:高中数学 来源: 题型:
【题目】已知平行四边形ABCD中,∠A=45°,且AB=BD=1,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图所示:
(1)求证:AB⊥CD;
(2)若M为AD的中点,求二面角A﹣BM﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面积S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知CD是等边三角形ABC的AB边上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
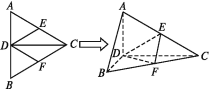
(1)求直线BC与平面DEF所成角的余弦值;
(2)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求f(x)在[t,t+2](t>0)上的最小值;
(2)若存在x ![]() 使不等式2f(x)≥g(x)成立,求实数a的取值范围.
使不等式2f(x)≥g(x)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个几何体三视图的正视图和侧视图为边长为2锐角60°的菱形,俯视图为正方形,则此几何体的内切球表面积为( ) 
A.8π
B.4π
C.3π
D.2π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
PM2.5 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲、乙两城市2013年2月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
(1)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(2)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(3)在乙城市15个监测数据中任取2个,设X为空气质量类别为优或良的天数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的长轴长是短轴长的两倍,且过点C(2,1),点C关于原点O的对称点为点D.
的长轴长是短轴长的两倍,且过点C(2,1),点C关于原点O的对称点为点D.
(1)求椭圆E的方程;
(2)点P在椭圆E上,直线CP和DP的斜率都存在且不为0,试问直线CP和DP的斜率之积是否为定值?若是,求此定值;若不是,请说明理由:
(3)平行于CD的直线l交椭圆E于M,N两点,求△CMN面积的最大值,并求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率等于![]() ,它的一个顶点恰好是抛物线x2=8
,它的一个顶点恰好是抛物线x2=8![]() y的焦点.
y的焦点.
(1)求椭圆C的标准方程;
(2)直线x=﹣2与椭圆交于P,Q两点,A,B是椭圆上位于直线x=﹣2两侧的动点,若直线AB的斜率为![]() ,求四边形APBQ面积的最大值.
,求四边形APBQ面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com