
【题目】已知四棱锥P-ABCD中,底面ABCD为直角梯形,![]() 平面ABCD,且
平面ABCD,且![]()
![]()
![]()
![]() .
.
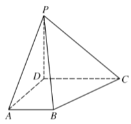
(1)求证:![]() 平面PBD;
平面PBD;
(2)若PB与平面ABCD所成的角为![]() ,求二面角D-PC-B的余弦值.
,求二面角D-PC-B的余弦值.
【答案】(1)证明见解析,(2)![]()
【解析】
(1)取CD的中点E,连接AE,BE,BD,证明四边形ABED为正方形,得到![]() ,再由线面垂直可得
,再由线面垂直可得![]() ,即可证明
,即可证明![]() 平面PBD,再证四边形ABCE为平行四边形,即可得证.
平面PBD,再证四边形ABCE为平行四边形,即可得证.
(2)以点D为坐标原点,分别以DA,DC,DP所在直线为x,y,z轴,建立空间直角坐标系,利用空间向量法求出二面角的余弦值.
解:(1)证明:取CD的中点E,连接AE,BE,BD.
![]()
![]() .
.
又![]()
![]() ,
,
![]() 四边形ABED为正方形,则
四边形ABED为正方形,则![]() .
.
![]() 平面ABCD,
平面ABCD,![]() 平面ABCD,
平面ABCD,
![]() .
.
![]()
![]() 平面PBD,
平面PBD,![]() 平面PBD.
平面PBD.
![]() 平面PBD.
平面PBD.
![]()
![]() ,
,
![]() 四边形ABCE为平行四边形,
四边形ABCE为平行四边形,
![]()
![]() 平面PBD.
平面PBD.
(2)![]() 平面ABCD,
平面ABCD,
![]() 为PB与平面ABCD所成的角,
为PB与平面ABCD所成的角,
即![]() ,则
,则![]() .
.
设![]() ,则
,则![]()
![]()
![]() .
.
以点D为坐标原点,分别以DA,DC,DP所在直线为x,y,z轴,建立如图所示的空间直角坐标系,
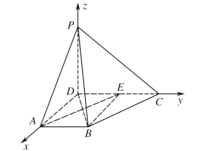
则![]()
![]()
![]()
![]() ,
,![]() .
.
![]()
![]() 平面PDC,
平面PDC,
![]() 平面PDC的一个法向量
平面PDC的一个法向量![]() .
.
设平面PBC的法向量![]() ,
,
![]()
![]() ,
,
则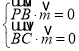
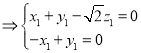 ,
,
取![]() ,则
,则![]() .
.
设二面角D-PC-B的平面角为![]() ,
,
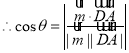
![]()
![]() .
.
由图可知二面角D-PC-B为锐角,
故二面角D-PC-B的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某地拟建造一座体育馆,其设计方案侧面的外轮廓线如图所示:曲线![]() 是以点
是以点![]() 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中![]()
![]() ,
,![]() 是圆的切线,且
是圆的切线,且![]() ,曲线
,曲线![]() 是抛物线
是抛物线![]()
![]() 的一部分,
的一部分,![]() ,且
,且![]() 恰好等于圆
恰好等于圆![]() 的半径.
的半径.
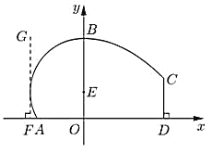
(1)若![]() 米,
米,![]() 米,求
米,求![]() 与
与![]() 的值;
的值;
(2)若体育馆侧面的最大宽度![]() 不超过75米,求
不超过75米,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公比大于
是公比大于![]() 的等比数列,
的等比数列,![]() 为数列
为数列![]() 的前
的前![]() 项和,
项和,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差数列.数列
成等差数列.数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 满足
满足![]() ,且
,且![]() ,
,
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令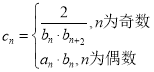 ,求数列
,求数列![]() 的前
的前![]() 项和为
项和为![]() ;
;
(3)将数列![]() ,
,![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面;当
放在前面;当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行排列,得到一个新的数列:
放在前面”的要求进行排列,得到一个新的数列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求这个新数列的前
,求这个新数列的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为两非零有理数列(即对任意的
为两非零有理数列(即对任意的![]() ,
,![]() ,
,![]() 均为有理数),
均为有理数),![]() 为一个无理数列(即对任意的
为一个无理数列(即对任意的![]() ,
,![]() 为无理数).
为无理数).
(1)已知![]() ,并且
,并且![]() 对任意的
对任意的![]() 恒成立,试求
恒成立,试求![]() 的通项公式;
的通项公式;
(2)若![]() 为有理数列,试证明:对任意的
为有理数列,试证明:对任意的![]() ,
,![]() 恒成立的充要条件为
恒成立的充要条件为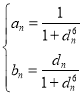 ;
;
(3)已知![]() ,
,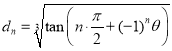 ,试计算
,试计算![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)试判断函数![]() 的单调性;
的单调性;
(Ⅱ)若函数![]()
![]() 在
在![]() 上有且仅有一个零点,
上有且仅有一个零点,
(i)求证:此零点是![]() 的极值点;
的极值点;
(ⅱ)求证:![]() .
.
(本题可能会用到的数据:![]()
![]()
![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大报告指出,在全面建成小康社会的决胜阶段,让贫困地区同全国人民共同进入全面小康社会是我们党的庄严承诺.在“脱真贫、真脱贫”的过程中,精准扶贫助推社会公平显得尤其重要.若某地区有100户贫困户,经过一年扶贫后,为了考查该地区的“精准扶贫”的成效![]() 该地区脱贫标准为“每户人均年收入不少于4000元”
该地区脱贫标准为“每户人均年收入不少于4000元”![]() ,现从该地区随机抽取A、B两个村庄,再从这两个村庄的贫困户中随机抽取20户,调查每户的现人均年收入,绘制如图所示的茎叶图
,现从该地区随机抽取A、B两个村庄,再从这两个村庄的贫困户中随机抽取20户,调查每户的现人均年收入,绘制如图所示的茎叶图![]() 单位:百元
单位:百元![]() .
.
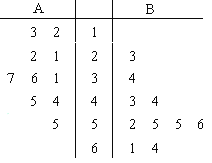
(1)观察茎叶图中的数据,判断哪个村庄扶贫成效较好?并说明理由;
(2)计划对没有脱贫的贫困户进一步实行“精准扶贫”,下一年的资金投入方案如下:对人均年收入不高于2000元的贫困户,每户每年增加扶贫资金5000元;对人均年收入高于2000元但不高于3000元的贫困户,每户每年增加扶贫资金3000元;对人均年收入高于3000元但不高于4000元的贫困户,每户每年增加扶贫资金1000元;对已经脱贫的贫困户不再增加扶贫资金投入.依据此方案,试估计下一年该地区共需要增加扶贫资金多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(a,b∈R)为奇函数.
,(a,b∈R)为奇函数.
(1)求b值;
(2)当a=﹣2时,存在x0∈[1,4]使得不等式f(x0)≤t成立,求实数t的取值范围;
(3)当a≥1时,求证:函数g(x)=f(2x)﹣c(c∈R)在区间(﹣∞,﹣1]上至多有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的所有项都是不等于
的所有项都是不等于![]() 的正数,
的正数,![]() 的前
的前![]() 项和为
项和为![]() ,已知点
,已知点![]() 在直线
在直线![]() 上(其中常数
上(其中常数![]() ,且
,且![]() )数列,又
)数列,又![]() .
.
(1)求证数列![]() 是等比数列;
是等比数列;
(2)如果![]() ,求实数
,求实数![]() 的值;
的值;
(3)若果存在![]() 使得点
使得点![]() 和
和![]() 都在直线在
都在直线在![]() 上,是否存在自然数
上,是否存在自然数![]() ,当
,当![]() (
(![]() )时,
)时,![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com