
【题目】关于x的不等式a![]() x2﹣3x+4≤b的解集为[a,b],则b-a=________.
x2﹣3x+4≤b的解集为[a,b],则b-a=________.
【答案】4
【解析】
设f(x)![]() x2﹣3x+4,其函数图象是抛物线,画两条与x轴平行的直线y=a和y=b,如果两直线与抛物线有两个交点,得到解集应该是两个区间;此不等式的解集为一个区间,所以两直线与抛物线不可能有两个交点,所以直线y=a应该与抛物线只有一个或没有交点,所以a小于或等于抛物线的最小值且a与b所对应的函数值相等且都等于b,利用f(b)=b求出b的值,由抛物线的对称轴求出a的值,从而求出结果.
x2﹣3x+4,其函数图象是抛物线,画两条与x轴平行的直线y=a和y=b,如果两直线与抛物线有两个交点,得到解集应该是两个区间;此不等式的解集为一个区间,所以两直线与抛物线不可能有两个交点,所以直线y=a应该与抛物线只有一个或没有交点,所以a小于或等于抛物线的最小值且a与b所对应的函数值相等且都等于b,利用f(b)=b求出b的值,由抛物线的对称轴求出a的值,从而求出结果.
解:画出函数f(x)=![]() x2﹣3x+4=
x2﹣3x+4=![]() (x-2)2+1的图象,如图,
(x-2)2+1的图象,如图,

可得f(x)min=f(2)=1,
由图象可知,若a>1,则不等式a≤![]() x2-3x+4≤b的解集分两段区域,不符合已知条件,
x2-3x+4≤b的解集分两段区域,不符合已知条件,
因此a≤1,此时a≤x2-3x+4恒成立.
又不等式a≤![]() x2-3x+4≤b的解集为[a,b],
x2-3x+4≤b的解集为[a,b],
所以a≤1<b,f(a)=f(b)=b,可得
由![]() b2-3b+4=b,化为3b2-16b+16=0,
b2-3b+4=b,化为3b2-16b+16=0,
解得b=![]() 或b=4.
或b=4.
当b=![]() 时,由
时,由![]() a2-3a+4-
a2-3a+4-![]() =0,解得a=
=0,解得a=![]() 或a=
或a=![]() ,
,
不符合题意,舍去,
所以b=4,此时a=0,
所以b-a=4.
故答案为:4


科目:高中数学 来源: 题型:
【题目】第二届中国国际进口博览会于2019年11月5日至10日在上海国家会展中心举行,来自151个国家和地区的3617家企业参展,规模和品质均超过首届.更多新产品、新技术、新服务“全球首发,中国首展”,专(业)精(品)尖(端)特(色)产品精华荟萃.某跨国公司带来了高端空调模型参展,通过展会调研,中国甲企业计划在2020年与该跨国公司合资生产此款空调.生产此款空调预计全年需投入固定成本260万元,每生产x千台空调,需另投入资金![]() 万元,且
万元,且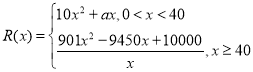 .经测算生产10千台空调需另投入的资金为4000万元.由调研知,每台空调售价为0.9万元时,当年内生产的空调当年能全部销售完.
.经测算生产10千台空调需另投入的资金为4000万元.由调研知,每台空调售价为0.9万元时,当年内生产的空调当年能全部销售完.
(1)求2020年的企业年利润![]() (万元)关于年产量x(千台)的函数关系式;
(万元)关于年产量x(千台)的函数关系式;
(2)2020年产量为多少(千台)时,企业所获年利润最大?最大年利润是多少?注:利润=销售额–成本
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商店出售茶壶和茶杯,茶壶定价每个20元,茶杯每个5元,该商店推出两种优惠办法:(1)买一个茶壶赠一个茶杯;(2)按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯数x个,付款y(元),分别建立两种优惠办法中y与x之间的函数关系式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抽样得到某次考试中高二年级某班![]() 名学生的数学成绩和物理成绩如下表:
名学生的数学成绩和物理成绩如下表:
学生编号 |
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
物里成绩 |
|
|
|
|
|
|
(1)在图中画出表中数据的散点图;
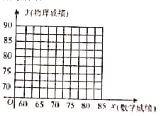
(2)建立![]() 关于
关于![]() 的回归方程:(系数保留到小数点后两位).
的回归方程:(系数保留到小数点后两位).
(3)如果某学生的数学成绩为![]() 分,预测他本次的物理成绩(成绩取整数).
分,预测他本次的物理成绩(成绩取整数).
参考公式:回归方程为![]() ,其中
,其中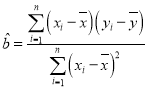 ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为
为![]() 轴上的点.
轴上的点.
(1)当![]() 时,过点
时,过点![]() 作直线
作直线![]() 与
与![]() 相切,求切线
相切,求切线![]() 的方程;
的方程;
(2)存在过点![]() 且倾斜角互补的两条直线
且倾斜角互补的两条直线![]() ,
,![]() ,若
,若![]() ,
,![]() 与
与![]() 分别交于
分别交于![]() ,
,![]() 和
和![]() ,
,![]() 四点,且
四点,且![]() 与
与![]() 的面积相等,求实数
的面积相等,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某民营企业生产A,B两种产品,根据市场调查与预测,A产品的利润y与投资x成正比,其关系如图甲,B产品的利润y与投资x的算术平方根成正比,其关系如图乙![]() 注:利润与投资单位为万元
注:利润与投资单位为万元![]()

![]() 分别将A,B两种产品的利润y表示为投资x的函数关系式;
分别将A,B两种产品的利润y表示为投资x的函数关系式;
![]() 该企业已筹集到10万元资金,并全部投入A,B两种产品的生产
该企业已筹集到10万元资金,并全部投入A,B两种产品的生产![]() 问:怎样分配这10万元资金,才能使企业获得最大利润,最大利润是多少万元?
问:怎样分配这10万元资金,才能使企业获得最大利润,最大利润是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com