
(本小题12分)在平面直角坐标系![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() .
.![]() 两点。
两点。
(1)求证:“如果直线![]() 过点
过点![]() ,那么
,那么![]() ”是真命题。
”是真命题。
(2)写出(1)中命题的逆命题(直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() .
.![]() 两点为大前提),判断它是真命题还是假命题,如果是真命题,写出证明过程;如果是假命题,举出反例说明。
两点为大前提),判断它是真命题还是假命题,如果是真命题,写出证明过程;如果是假命题,举出反例说明。
证明:(1)设过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于点
于点![]() ,
,![]() ,
,
当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,此时,直线
,此时,直线![]() 与抛物线相交于
与抛物线相交于![]() ,
,![]() 。----------------2分
。----------------2分
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,其中
,其中![]()
由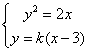 得
得![]() -------------------4分
-------------------4分
又![]()
![]()
综上,“直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() .
.![]() 两点,如果直线
两点,如果直线![]() 过点
过点![]() ,那么
,那么![]() ”是真命题。---------------------6分(注,如果设
”是真命题。---------------------6分(注,如果设![]() )
)
(2) (1)中命题的逆命题是:“直线![]() 交抛物线
交抛物线![]() 于
于![]() .
.![]() 两点,如果
两点,如果![]() ,那么直线
,那么直线![]() 过点
过点![]() ”--------------------8分
”--------------------8分
该命题是个假命题。-----------------------9分
例如:取抛物线上的点![]()
![]() ,直线AB的方程为
,直线AB的方程为![]() ,而点(3,0)不在直线AB上。--------------------12分
,而点(3,0)不在直线AB上。--------------------12分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
(09年长沙一中第八次月考理)(本小题满分12分)我校文化体育艺术节的乒乓球决赛在甲乙两人中进行,比赛规则如下:比赛采用7局4胜制(先胜4局这获胜即比赛结束),在每一局比赛中,先得11分的一方为胜方;比赛没有平局,10平后,先连得2分的一方为胜方![]()
(1)根据以往战况,每局比赛甲胜乙的概率为0.6,设比赛的场数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)如图在空间直角坐标系中![]() ,原点
,原点![]() 是
是![]() 的中点,点
的中点,点![]() 的坐标是(
的坐标是(![]() ),点
),点![]() 在平面
在平面![]() 上,且
上,且![]() ,
,![]() .
.
(I)求向量![]() 的坐标;
的坐标;![]()
![]()
![]()
(Ⅱ)设向量![]() 和
和![]() 的夹角为
的夹角为![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省高三二轮复习综合测试数学理卷 题型:解答题
(本小题满分12分)
一个多面体的直观图和三视图如图所示
 (1)求证:
(1)求证: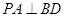 ;(2)是否在线段
;(2)是否在线段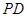 上存在一
上存在一 点,使二面角
点,使二面角 的平
的平
面角为 ,设
,设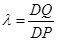 ,若存在,求
,若存在,求 ;若不存在,说明理由
;若不存在,说明理由
 |
|||
 |
|||
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市高三起点考试理科数学卷 题型:解答题
(本小题满分12分)
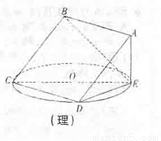
如右图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,AE=3,圆O的直径为9。
(1)求证:平面ABCD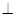 平在ADE;
平在ADE;
(2)求二面角D—BC—E的平面角的正切值;
查看答案和解析>>
科目:高中数学 来源:2010年海南省高二上学期第二次月考理科数学卷 题型:解答题
(本小题满分12分)某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其他两观测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com