
| 1 |
| 3 |
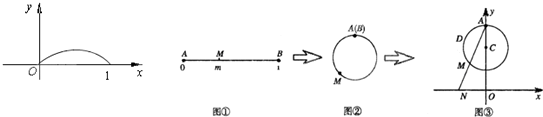
| CM |
| NO |
| AM |
| AO |
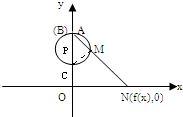
| CM |
| NO |
| AM |
| AO |
| 1 |
| π |
| 1 |
| π |
| 1 |
| π |
| cosmπ |
| sinmπ |
| 1 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| cosmπ |
| sinmπ |


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
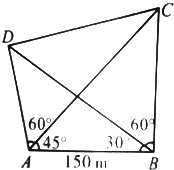 如图,A、B、C、D是河两岸的四根电线杆,A、B在河这边,C、D在河对岸,现在距离A处150m的B处测得∠ABD=30°,∠DBC=60°,而在A处测得∠BAC=45°,∠CAD=60°,求C、D两点间的距离.(已知A、B、C、D在同一平面内).
如图,A、B、C、D是河两岸的四根电线杆,A、B在河这边,C、D在河对岸,现在距离A处150m的B处测得∠ABD=30°,∠DBC=60°,而在A处测得∠BAC=45°,∠CAD=60°,求C、D两点间的距离.(已知A、B、C、D在同一平面内).查看答案和解析>>
科目:高中数学 来源: 题型:
| A、推理的形式不符合三段论的要求 |
| B、大前提错误 |
| C、小前提错误 |
| D、推理的结果错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:
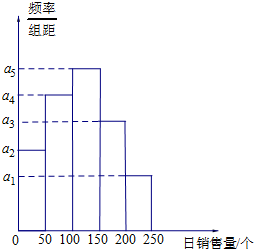 广州某商场根据以往某种商品的销售记录,绘制了日销售量的频率分布表(如表)和频率分布直方图(如图).
广州某商场根据以往某种商品的销售记录,绘制了日销售量的频率分布表(如表)和频率分布直方图(如图). | 分组 | 频数 | 频率 |
| [0,50] | n1 | 0.15 |
| (50,100] | n2 | 0.25 |
| (100,150] | n3 | 0.30 |
| (150,200] | n4 | 0.20 |
| (200,250] | n5 | 0.10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| b |
| a |
| 1 |
| 9 |
| PQ |
| 6 |
| 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| AF |
| FB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com