
【题目】已知函数![]()
![]() .
.
(1)当![]() 时,
时,
①求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
②求函数![]() 在区间
在区间![]() 上的值域.
上的值域.
(2)对于任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ②
②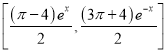 ;(2)
;(2)![]() .
.
【解析】试题分析:
(1)由题意可得函数的解析式![]() ,
,
①利用导数研究切线方程可得曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
②利用导函数研究函数的单调性可得![]() 在区间
在区间![]() 上的值域为
上的值域为 .
.
(2)原问题等价于![]() .构造函数
.构造函数![]() ,分类讨论可得实数
,分类讨论可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)当![]() 时,
时, ![]() ,
,
①![]() ,由
,由![]() ,
, ![]() ,
,
则曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,整理为:
,整理为: ![]() .
.
②令![]() ,有
,有![]() ,
,
当![]() 时,
时, ![]() ,
,
当![]() 时
时![]() ,得
,得![]() ,解得:
,解得: ![]() ,
,
故当![]() 时,
时, ![]() ,可得
,可得![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
![]()
![]() ,
, ![]()
![]() ,
,
故函数![]() 在区间
在区间![]() 上的值域为
上的值域为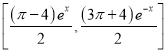 .
.
(2)由![]() ,有
,有![]() ,故
,故![]() 可化为
可化为![]() .
.
整理得: ![]() .
.
即函数![]() 在区间
在区间![]() 为增函数,
为增函数,
![]()
![]() ,
,
![]() ,故当
,故当![]() 时,
时, ![]() ,即
,即![]() ,
,
①当![]() 时,
时, ![]() ;
;
②当![]() 时,整理为:
时,整理为: ![]() ,
,
令![]() ,有
,有![]()
![]() ,
,
当![]() ,
, ![]() ,
, ![]() ,有
,有![]() ,
,
当![]() 时,函数
时,函数![]() 单调递减,故
单调递减,故![]() ,
,
故有: ![]() ,可得
,可得![]() .
.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2. (Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求平面PAD和平面PBE所成二面角(锐角)的余弦值.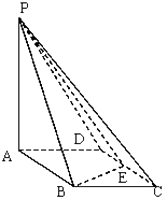
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了引导居民合理用电,国家决定实行合理的阶梯电价,居民用电原则上以住宅为单位(一套住宅为一户).
阶梯级别 | 第一阶梯 | 第二阶梯 | 第三阶梯 |
月用电范围(度) | (0,210] | (210,400] |
|
某市随机抽取10户同一个月的用电情况,得到统计表如下:
居民用电户编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用电量(度) | 53 | 86 | 90 | 124 | 132 | 200 | 215 | 225 | 300 | 410 |
若规定第一阶梯电价每度0.5元,第二阶梯超出第一阶梯的部分每度0.6元,第三阶梯超出第二阶梯的部分每度0.8元,试计算A居民用电户用电410度时应电费多少元?
现要在这10户家庭中任意选取3户,求取到第二阶梯电量的户数的分布列与期望;
以表中抽到的10户作为样本估计全市的居民用电,现从全市中依次抽取10户,若抽到![]() 户用电量为第一阶梯的可能性最大,求
户用电量为第一阶梯的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强高考与高中学习的关联度,考生总成绩由统一高考的语文、数学、外语3个科目成绩和高中学业水平考试3个科目成绩组成.保持统一高考的语文、数学、外语科目不变,分值不变,不分文理科,外语科目提供两次考试机会.计入总成绩的高中学业水平考试科目,由考生根据报考高校要求和自身特长,在思想政治、历史、地理、物理、化学、生物、信息技术七科目中自主选择三科.
(1)某高校某专业要求选考科目物理,考生若要报考该校该专业,则有多少种选考科目的选择;
(2)甲、乙、丙三名同学都选择了物理、化学、历史组合,各学科成绩达到二级的概率都是0.8,且三人约定如果达到二级不参加第二次考试,达不到二级参加第二次考试,如果设甲、乙、丙参加第二次考试的总次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位建造一间背面靠墙的小房,地面面积为12m2 , 房屋正面每平方米造价为1200元,房屋侧面每平方米造价为800元,屋顶的造价为5800元,如果墙高为3m,且不计房屋背面和地面的费用,设房屋正面地面的边长为xm,房屋的总造价为y元.
(1)求y用x表示的函数关系式;
(2)怎样设计房屋能使总造价最低?最低总造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)令![]() ,区间
,区间 ,
, ![]() 为自然对数的底数。
为自然对数的底数。
(ⅰ)若函数![]() 在区间
在区间![]() 上有两个极值,求实数
上有两个极值,求实数![]() 的取值范围;
的取值范围;
(ⅱ)设函数![]() 在区间
在区间![]() 上的两个极值分别为
上的两个极值分别为![]() 和
和![]() ,
,
求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}为单调递增数列,首项a1=4,且满足an+12+an2+16=8(an+1+an)+2an+1an , n∈N* , 则a1﹣a2+a3﹣a4+…+a2n﹣1﹣a2n=( )
A.﹣2n(2n﹣1)
B.﹣3n(n+3)
C.﹣4n(2n+1)
D.﹣6n(n+1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com