
思路分析:条件是用正切表达的α与β的关系,欲证目标是正弦表达的α与β的关系,可用条件![]() tan2β=12(tan2α-1)把tan2β
tan2β=12(tan2α-1)把tan2β![]() sin2β证出目标,也可找出α与β的关系证出目标.
sin2β证出目标,也可找出α与β的关系证出目标.
证法一:因为tan2α=2tan2β+1,所以tan2β=![]() .
.
又sin2β=tan2β·cos2β=![]() =
=![]() =
=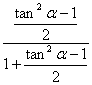 =
=
![]() =
=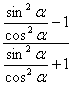 =sin2α-cos2α=2sin2α-1,所以sin2β=2sin2α-1.
=sin2α-cos2α=2sin2α-1,所以sin2β=2sin2α-1.
证法二:2sin2α-1=![]() -1=
-1=![]() -1=
-1=
![]() =
=![]() =sin2β,所以原等式成立.
=sin2β,所以原等式成立.
证法三:因为tan2α=2tan2β+1,
所以![]() =
=![]() +1=
+1=![]() .
.
所以![]() .
.
所sin2α(1-sin2β)=(1-sin2α)(1+sin2β).
所以sin2β=2sin2α-1.
证法四:因为tan2α=2tan2β+1,
所以1+tan2α=2(tan2β+1).
所以sec2α=2sec2β.
所以2cos2α=cos2β.
所以2(1-sin2α)=1-sin2β.
所以sin2β=2sin2α-1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com