
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,已知asinB=bsin(A![]() ).
).
(1)求A;
(2)D是线段BC上的点,若AD=BD=2,CD=3,求△ADC的面积.
【答案】(1)A![]() ;(2)
;(2)![]() .
.
【解析】
(1)首先利用正弦定理可得asinB=bsinA,然后利用两角差的正弦公式展开化简即可求解.
(2)设∠B=θ,![]() ,由题意可得∠BAD=θ,∠ADC=2θ,∠DAC
,由题意可得∠BAD=θ,∠ADC=2θ,∠DAC![]() θ,在△ADC中,利用正弦定理可得sinθ
θ,在△ADC中,利用正弦定理可得sinθ![]() cosθ,根据同角三角函数的基本关系求出sin2θ,再利用三角形的面积公式即可求解.
cosθ,根据同角三角函数的基本关系求出sin2θ,再利用三角形的面积公式即可求解.
(1)由正弦定理可得asinB=bsinA,
则有bsinA=b(![]() sinA
sinA![]() cosA),化简可得
cosA),化简可得![]() sinA
sinA![]() cosA,
cosA,
可得tanA![]() ,
,
因为A∈(0,π),
所以A![]() .
.
(2)设∠B=θ,![]() ,由题意可得∠BAD=θ,∠ADC=2θ,
,由题意可得∠BAD=θ,∠ADC=2θ,
∠DAC![]() θ,∠ACD
θ,∠ACD![]() θ,
θ,
在△ADC中,![]() ,则
,则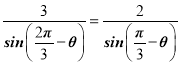 ,
,
所以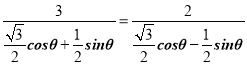 ,可得sinθ
,可得sinθ![]() cosθ,
cosθ,
又因为sin2θ+cos2θ=1,可得sinθ![]() ,cosθ
,cosθ![]() ,
,
则sin2θ=2sinθcosθ![]() ,
,
所以S△ADC![]() sin∠ADC
sin∠ADC![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其它各面用钢筋网围成.
(1)现有可围![]() 长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?
长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?
(2)若使每间虎笼面积为![]() ,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋网总长最小?
,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋网总长最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
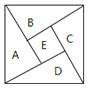
【题目】如图为我国数学家赵爽![]() 约3世纪初
约3世纪初![]() 在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则
在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则![]() 区域涂色不相同的概率为
区域涂色不相同的概率为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】谢尔宾斯基三角形(英语:Sierpinskitriangle)是一种分形,由波兰数学家谢尔宾斯基在1915年提出.具体操作是:先取一个实心正三角形(图1),挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形)(图2),然后在剩下的三个小三角形中又各挖去一个“中心三角形”(图3),我们用黑色三角形代表剩下的面积,用上面的方法可以无限连续地作下去.若设操作次数为3(每挖去一次中心三角形算一次操作),在图中随机选取一个点,则此点取自黑色三角形的概率为__________.
![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】探月工程“嫦娥四号”探测器于2018年12月8日成功发射,实现了人类首次月球背面软着陆.以嫦娥四号为任务圆满成功为标志,我国探月工程四期和深空探测工程全面拉开序幕.根据部署,我国探月工程到2020年前将实现“绕、落、回”三步走目标.为了实现目标,各科研团队进行积极的备战工作.某科研团队现正准备攻克甲、乙、丙三项新技术,甲、乙、丙三项新技术独立被攻克的概率分别为![]() ,若甲、乙、丙三项新技术被攻克,分别可获得科研经费
,若甲、乙、丙三项新技术被攻克,分别可获得科研经费![]() 万,
万,![]() 万,
万,![]() 万.若其中某项新技术未被攻克,则该项新技术没有对应的科研经费.
万.若其中某项新技术未被攻克,则该项新技术没有对应的科研经费.
(1)求该科研团队获得![]() 万科研经费的概率;
万科研经费的概率;
(2)记该科研团队获得的科研经费为随机变量![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ),
),![]() .
.
(1)若![]() 的图象在
的图象在![]() 处的切线恰好也是
处的切线恰好也是![]() 图象的切线.
图象的切线.
①求实数![]() 的值;
的值;
②若方程![]() 在区间
在区间![]() 内有唯一实数解,求实数
内有唯一实数解,求实数![]() 的取值范围.
的取值范围.
(2)当![]() 时,求证:对于区间
时,求证:对于区间![]() 上的任意两个不相等的实数
上的任意两个不相等的实数![]() ,
, ![]() ,都有
,都有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的焦点为F,过点F的直线交抛物线于A,B两点.
的焦点为F,过点F的直线交抛物线于A,B两点.
(1)若![]() ,求直线AB的斜率;
,求直线AB的斜率;
(2)设点M在线段AB上运动,原点O关于点M的对称点为C,求四边形OACB面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com