
【题目】在四棱柱![]() 中,已知底面
中,已知底面![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,M,N分别是棱
,M,N分别是棱![]() ,
,![]() 的中点
的中点
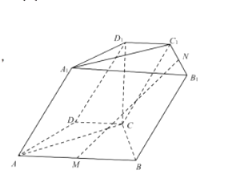
(1)证明:直线![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,且
,且![]() ,求经过点A,M,N的平面
,求经过点A,M,N的平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点P,连结
的中点P,连结![]() ,证得
,证得![]() ,利用线平行的判定定理,即可证得直线
,利用线平行的判定定理,即可证得直线![]() 平面
平面![]() ;
;
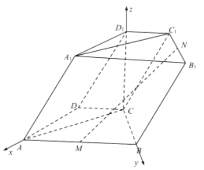
(2)以![]() 所在的直线为
所在的直线为![]() 轴,建立如图所示的空间直角坐标系,分别求得平面
轴,建立如图所示的空间直角坐标系,分别求得平面![]() 和平面
和平面![]() 的一个法向量,利用向量的夹角公式,即可求解.
的一个法向量,利用向量的夹角公式,即可求解.
(1)取![]() 的中点P,连结
的中点P,连结![]() ,
,![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以![]() ,且
,且![]() ,所以
,所以![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
因为![]() 平面
平面![]() ,所以直线
,所以直线![]() 平面
平面![]() .
.
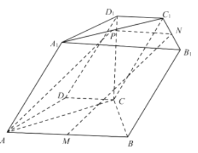
(2)连结![]() ,
,
由己知可得,![]() ,所以
,所以![]() 为等边三角形,
为等边三角形,
所以![]() ,
,![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以![]() ,
,
分别以![]() 所在的直线为
所在的直线为![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
则![]() ,
,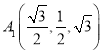 ,
,![]() ,
,![]() ,
,![]() ,
,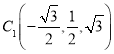 ,
,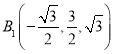 , 所以
, 所以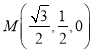 ,
,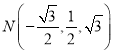 ,
,
可得![]() ,
,![]() ,
,![]() ,
,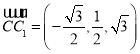 .
.
设平面![]() 的法向量为
的法向量为![]() ,所以
,所以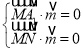 ,即
,即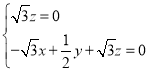 ,取
,取![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,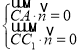 ,即
,即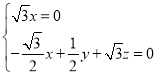 ,
,
取![]() ,可得
,可得![]() ,所以
,所以![]() ,
,
设平面![]() 与平面
与平面![]() 所成二面角的大小为
所成二面角的大小为![]() ,
,
所以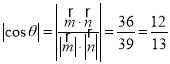 ,则
,则![]()
所以平面![]() 与平面
与平面![]() 所成二面角的正弦值为
所成二面角的正弦值为![]() .
.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 经过点
经过点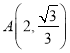 ,两个焦点为
,两个焦点为![]() ,
,![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() 是
是![]() 上一点,直线
上一点,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,证明:当
,证明:当![]() 点在
点在![]() 上移动时,
上移动时,![]() 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为:
的参数方程为: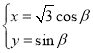 ,(
,(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为
轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为![]()
(1)求曲线![]() 和直线l的直角坐标方程;
和直线l的直角坐标方程;
(2)若点![]() 在曲线
在曲线![]() 上,且点
上,且点![]() 到直线l的距离最小,求点
到直线l的距离最小,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() ,
,![]() 满足:对任意正整数
满足:对任意正整数![]() ,都有
,都有![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() ,
,![]() ,
,![]() 成等比数列,且
成等比数列,且![]() ,
,![]() .
.
(Ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(Ⅱ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅲ)设![]() =
=![]() +
+![]() +…+
+…+![]() ,如果对任意的正整数
,如果对任意的正整数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=2,E是CD的中点,现以AE为折痕将△DAE向上折起,D变为D',使得平面D'AE⊥平面ABCE.
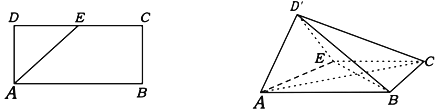
(1)求证:平面ABD'⊥平面BD'E;
(2)求直线CE与平面BCD'所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
求分数在[120,130)内的频率,并补全这个频
率分布直方图;
统计方法中,同一组数据常用该组区间的中点
值作为代表,据此估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段[120,130)内的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com