(I)证明:∵面ABC⊥面BCQ
又CQ⊥BC
∴CQ⊥面ABC
∴CQ⊥AB(5分)
(Ⅱ)解:取BC的中点O,BD的中点E,如图以OB所在直线为x轴,以OE所在直线为y轴,以OA所在直线为z轴,建立空间直角坐标系.(6分)
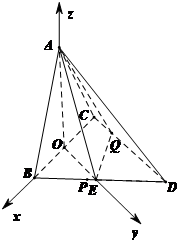
不妨设BC=2,则A(0,0,1),D(-1,2,0),P(x,1-x,0),(8分)
由|AP|=|DP|即x
2+(1-x)
2+1=(x+1)
2+(x+1)
2,
解得x=0,所以P(0,1,0),(10分)
故

=(0,1,-1)
设

=(x,y,z)为平面ACQ的一个法向量,
因为

=(-1,0,-1),
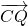
=
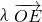
=λ(0,1,0)
由

即
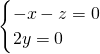
所以

=(1,0,-1)(12分)
设直线AP与平面ACQ所成的角为α
则Sinα=|cos<AP,n>|=

所以α=

即直线AP与平面ACQ所成的角为V(14分)
分析:(I)由已知中面ABC⊥面BCQ,及=∠BCD=90°,我们根据面面垂直的性质定理,我们易得CQ⊥面ABC,进而根据线面垂直的定义,即可得到AB⊥CQ;
(Ⅱ)以BC的中点O,BD的中点E,如图以OB所在直线为x轴,以OE所在直线为y轴,以OA所在直线为z轴,建立空间直角坐标系,求出各顶点的坐标,进而求出直线AP的方向向量及平面ACQ的法向量,根据向量法求线面夹角的步骤,即可得到答案.
点评:本题考查的知识点是用空间向量求直线与平面的夹角,直线与平面垂直的性质,直线与平面所成的角,熟练掌握空间向量法求线线夹角、线面夹角及两面角的方法步骤是解答此类问题的关键.

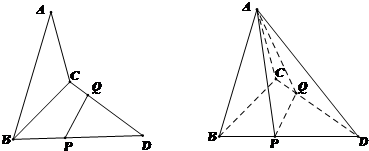 如图,已知三角形△ABC与△BCD所在平面互相垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.
如图,已知三角形△ABC与△BCD所在平面互相垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合. 不妨设BC=2,则A(0,0,1),D(-1,2,0),P(x,1-x,0),(8分)
不妨设BC=2,则A(0,0,1),D(-1,2,0),P(x,1-x,0),(8分) =(0,1,-1)
=(0,1,-1) =(x,y,z)为平面ACQ的一个法向量,
=(x,y,z)为平面ACQ的一个法向量, =(-1,0,-1),
=(-1,0,-1),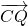 =
=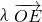 =λ(0,1,0)
=λ(0,1,0) 即
即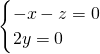
 =(1,0,-1)(12分)
=(1,0,-1)(12分)



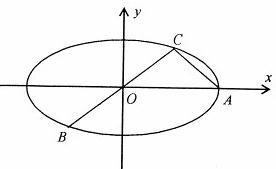 如图:已知椭圆A,B,C是长轴长为4的椭圆上三点,点A是长轴的一个端点,BC过椭圆的中心O,且
如图:已知椭圆A,B,C是长轴长为4的椭圆上三点,点A是长轴的一个端点,BC过椭圆的中心O,且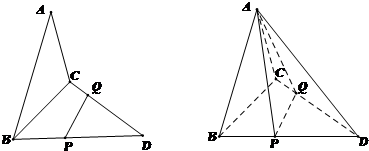 如图,已知三角形△ABC与△BCD所在平面互相垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.
如图,已知三角形△ABC与△BCD所在平面互相垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合. (2011•泉州模拟)如图,已知三角形ABC的三边AB=4,AC=5,BC=3,椭圆M以A、B为焦点且经过点C.
(2011•泉州模拟)如图,已知三角形ABC的三边AB=4,AC=5,BC=3,椭圆M以A、B为焦点且经过点C.