
����Ŀ����ֱ֪��l��x��2y��2m��2��0��
(1)�����(2��3)����ֱ��l��ֱ��ֱ�ߵķ��̣�
(2)��ֱ��l������������Χ�ɵ������ε��������4����ʵ��m��ȡֵ��Χ��
���𰸡���1��![]() ����2��
����2��![]()
�������������������1����ֱ��![]() ��б��Ϊ
��б��Ϊ![]() ���ɵ�����ֱ�ߵ�б��Ϊ
���ɵ�����ֱ�ߵ�б��Ϊ![]() �������бʽ���̣��ɵô𰸣���2��ֱ��
�������бʽ���̣��ɵô𰸣���2��ֱ��![]() ����������Ľ���ֱ�Ϊ
����������Ľ���ֱ�Ϊ![]() ������Χ�ɵ������ε����Ϊ
������Χ�ɵ������ε����Ϊ![]() ������ֱ��
������ֱ��![]() ������������Χ�ɵ������ε����Ϊ����
������������Χ�ɵ������ε����Ϊ����![]() �����첻��ʽ����ô�.
�����첻��ʽ����ô�.
���������(1)��ֱ��l��ֱ��ֱ�ߵ�б��Ϊ��2��
��Ϊ��(2��3)�ڸ�ֱ���ϣ���������ֱ�߷���Ϊy��3����2(x��2)��
�������ֱ�߷���Ϊ2x��y��7��0��
(2) ֱ��l����������Ľ���ֱ�Ϊ(��2m��2��0)��(0��m��1)��
����Χ�ɵ������ε����Ϊ![]() ��|��2m��2|��|m��1|��
��|��2m��2|��|m��1|��
�������֪![]() ��|��2m��2|��|m��1|��4�������(m��1)2��4��
��|��2m��2|��|m��1|��4�������(m��1)2��4��
���m��3��m����1��
����ʵ��m��ȡֵ��Χ��(��������1)��(3������)��
�������㾦��������Ҫ����ֱ�ߵķ��̣�����ֱ��ƽ����б�ʵĹ�ϵ�����ڼ���. ��ֱ��λ�ù�ϵ�Ŀ������ȵ����ⷽ��֮һ�����������Լ���Ϊ������Ҫ������ֱ�ߴ�ֱ����ֱ��ƽ�����������ϵ����б�ʴ��ڵ�ǰ���£���1��![]() ����2��
����2��![]() ���������⾡�ܼ�ȴ���׳������ر�����������б�ʲ����ڵ��������һ��һ�����ܵ�������.
���������⾡�ܼ�ȴ���׳������ر�����������б�ʲ����ڵ��������һ��һ�����ܵ�������.
�����͡������
��������
18
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪����ԭ��O��ֱ��
�У���֪����ԭ��O��ֱ��![]() ��Բ
��Բ![]() ����
����![]() ���㡣
���㡣
��1����ֱ��![]() ��Բ
��Բ![]() ���У��е�ΪB����ֱ��
���У��е�ΪB����ֱ��![]() �ķ��̣�
�ķ��̣�
��2����![]() ����ֱ��
����ֱ��![]() �ķ��̣�
�ķ��̣�
���𰸡���1��![]() ����2��
����2��![]()
�������������������1����ֱ����Բ���У���Բ�ĵ�ֱ�ߵľ���![]() ���з������
���з������![]() ��ֵ���Ӷ����ֱ��
��ֵ���Ӷ����ֱ��![]() �ķ��̣���2������
�ķ��̣���2������![]() ���е�
���е�![]() �����
�����![]() ���������ֱ�ߵķ��̣�����Բ�ĵ�ֱ��
���������ֱ�ߵķ��̣�����Բ�ĵ�ֱ��![]() �ľ���
�ľ���![]() ���ɶ����з��̣��������
���ɶ����з��̣��������![]() �ķ���.
�ķ���.
�����������1�������е�![]() ����ã�
����ã� ![]() ��
��
���![]() ������
������![]() ����
����![]()
��ֱ��![]() ��Բ����е�
��Բ����е�![]() ����
����![]()
��2��ȡAB�е�M����![]() ����
����![]() ������
������![]() ,
,
��![]() ��Բ�ĵ�ֱ��
��Բ�ĵ�ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]() ���ɹ��ɶ����ã�
���ɹ��ɶ����ã� ![]() ��
��
���![]() ��
��
������ֱ�ߵķ���Ϊ![]() ��
�� ![]() �����
�����![]() ��
�� ![]()


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ij����һ��յ�![]() ������
������![]() ��
�� ![]() ��
�� ![]() �������������滮�����յظ����һ�����ξ��㣬�����м���һ���˹���
�������������滮�����յظ����һ�����ξ��㣬�����м���һ���˹���![]() ������
������![]() ���ڱ�
���ڱ�![]() �ϣ���
�ϣ���![]() ���ڳ��������ѷ���
���ڳ��������ѷ���![]() �ش����γɼ�ɽ��ʣ�µ�
�ش����γɼ�ɽ��ʣ�µ�![]() �ش������ͯ���ֳ�. Ϊ��ȫ���������
�ش������ͯ���ֳ�. Ϊ��ȫ���������![]() ����Χ��װ������.
����Χ��װ������.
��1����![]() ʱ������������ܳ��ȣ�
ʱ������������ܳ��ȣ�
��2����Ҫ�����˹����õ�![]() ������ǶѼ�ɽ�õ�
������ǶѼ�ɽ�õ�![]() �������
�������![]() ������ȷ��
������ȷ��![]() �Ĵ�С��
�Ĵ�С��
��3��Ϊ��ʡͶ���ʽ��˹���![]() �����Ҫ������С����������ʩ����������ʹ
�����Ҫ������С����������ʩ����������ʹ![]() �������С����С����Ƕ��٣�
�������С����С����Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������![]() �У�
�� ![]() ����������
����������![]() ������
������![]() ��
�� ![]() ����
����![]() ����ʹ��
����ʹ��![]() ������n�����ֵΪ
������n�����ֵΪ![]() ��
��
����������{an}Ϊ1��3��5��7������д��b1��b2��b3��ֵ��
������{an}Ϊ�ȱ����У���a2=2����b1+b2+b3+��+b50��ֵ��
������{bn}Ϊ�Ȳ����У�������п��ܵ�����{an}��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ι���ѧ�������ϣ������ĸ����ҵ���λ��������������һ��Բ����Ϊ��ʹ�����ܹ����ɽ�̸�������˽��������£�
�����й��ˣ�����˵Ӣ�
���Ƿ����ˣ�����˵���
����Ӣ���ˣ�����˵���
�����ձ��ˣ�����˵���
���Ƿ����ˣ�����˵���
������λ��������λ˳��ӦΪ�� ��
A.�ױ�������
B.��������
C.���ұ�����
D.�ױ����Ҷ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ԲE�� ![]() +
+ ![]() =1��a��b��0������A����2��0�����ҵ㣨��1��
=1��a��b��0������A����2��0�����ҵ㣨��1�� ![]() ������Բ�ϣ�F1��F2�ֱ�����Բ�����ҽ��㣮����A��б��Ϊk��k��0����ֱ�߽���ԲE����һ��B��ֱ��BF2����ԲE�ڵ�C��
������Բ�ϣ�F1��F2�ֱ�����Բ�����ҽ��㣮����A��б��Ϊk��k��0����ֱ�߽���ԲE����һ��B��ֱ��BF2����ԲE�ڵ�C��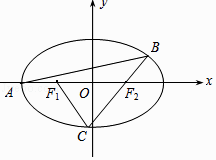
��1������ԲE�ı����̣�
��2������CF1F2Ϊ���������Σ����B�����ꣻ
��3����F1C��AB����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��P��0��1����ԲC��x2+y2+2mx��2y+m2��4m+1=0�ڣ������ڹ���P��ֱ�߽�ԲC��A��B���㣬�ҡ�PBC������ǡ�PAC�������2������ʵ��m��ȡֵ��ΧΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ABC��90����AB��![]() ��BC��1��PΪ��ABC��һ�㣬��BPC��90��.
��BC��1��PΪ��ABC��һ�㣬��BPC��90��.
(1)��PB��![]() ����PA��
����PA��
(2)����APB��150������tan��PBA.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ��k��
��k�� ![]() +lnx������x=2�Ǻ���f��x����Ψһһ����ֵ�㣬��ʵ��k��ȡֵ��ΧΪ�� ��
+lnx������x=2�Ǻ���f��x����Ψһһ����ֵ�㣬��ʵ��k��ȡֵ��ΧΪ�� ��
A.�����ޣ�e]
B.[0��e]
C.�����ޣ�e��
D.[0��e��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1���жϲ�֤������![]() ����ż�ԣ�
����ż�ԣ�
��2���жϵ�![]() ʱ����
ʱ����![]() �ĵ����ԣ����ö���֤����
�ĵ����ԣ����ö���֤����
��3����![]() ������Ϊ
������Ϊ![]() ���ⲻ��ʽ
���ⲻ��ʽ![]() .
.
���𰸡���1���溯����2����������3��![]()
�������������������1���ж���֤����������ż�ԣ�����Ҫȷ�������Ķ������Ƿ����ԭ��Գƣ����ж�f(-x)��f(x)�Ĺ�ϵ������Զ������ϵ�����x��������f(-x)=f(x)����ż���������f(-x)=-f(x)�����溯���������Ƿ����ż��������2�������������Զ���֤�������ԣ������裬��������жϣ��½���������衣��3���ɣ�1����2���溯��![]() �ڣ�-1��1��Ϊ����������
�ڣ�-1��1��Ϊ����������
ԭ����ʽ����Ϊf(2x-1)<-f(x),��f(2x-1)<f(-x),���ɺ����ĵ����Լ����壨-1��1������x��Χ��
�����������1������![]() Ϊ�溯����֤�����£�
Ϊ�溯����֤�����£�
![]() ������Ϊ
������Ϊ![]()
��![]()
![]() Ϊ�溯��
Ϊ�溯��
��2������![]() �ڣ�-1��1��Ϊ����������֤�����£�
�ڣ�-1��1��Ϊ����������֤�����£�
��ȡ![]() ����
����


![]()
![]() ��
�� ![]()

��![]()
��![]() �ڣ�-1��1����Ϊ������
�ڣ�-1��1����Ϊ������
��3���ɣ�1������2���ɵ�
![]() ��
��
 ��ã�
��ã� ![]()
���ԣ�ԭ����ʽ�Ľ⼯Ϊ![]()
���㾦��
��1����ż�ԣ��ж���֤����������ż�ԣ�����Ҫȷ�������Ķ������Ƿ����ԭ��Գƣ����ж�f(-x)��f(x)�Ĺ�ϵ������Զ������ϵ�����x��������f(-x)=f(x)����ż���������f(-x)=-f(x)�����溯���������Ƿ����ż������
��2�������ԣ������������Զ���֤�������ԣ������裬��������ţ��½���������衣
�����͡������
��������
22
����Ŀ����֪����![]() .
.
��1����![]() �Ķ������ֵ�����
�Ķ������ֵ�����![]() ����ʵ��
����ʵ��![]() ��ֵ��
��ֵ��
��2����![]() ������
������![]() ���Ǽ��������Ҷ������
���Ǽ��������Ҷ������![]() ������
������![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ���Ҷ������
���Ҷ������![]() ��������
��������![]() ��ʹ��
��ʹ��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com