
【题目】若函数f(x)= ![]() x3+x2﹣ax+3a在区间[1,2]上单调递增,则实数a的取值范围是 .
x3+x2﹣ax+3a在区间[1,2]上单调递增,则实数a的取值范围是 .
 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线E:y2=2px(p>0)的准线与x轴交于点K,过点K作圆(x﹣5)2+y2=9的两条切线,切点为M,N,|MN|=3 ![]()
(1)求抛物线E的方程;
(2)设A,B是抛物线E上分别位于x轴两侧的两个动点,且 ![]() (其中O为坐标原点).
(其中O为坐标原点).
①求证:直线AB必过定点,并求出该定点Q的坐标;
②过点Q作AB的垂线与抛物线交于G,D两点,求四边形AGBD面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某市民众对某项公共政策的态度,在该市随机抽取了![]() 名市民进行调查,做出了他们的月收入(单位:百元,范围:
名市民进行调查,做出了他们的月收入(单位:百元,范围:![]() )的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:
)的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:
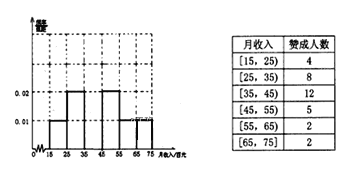
(1)求月收入在![]() 内的频率,并补全这个频率分布直方图,并在图中标出相应纵坐标;
内的频率,并补全这个频率分布直方图,并在图中标出相应纵坐标;
(2)根据频率分布直方图估计这![]() 人的平均月收入;
人的平均月收入;
(3)若从月收入(单位:百元)在![]() 的被调查者中随机选取
的被调查者中随机选取![]() 人,求
人,求![]() 人都不赞成的概率.
人都不赞成的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知C= ![]() ,向量
,向量 ![]() =(sinA,1),
=(sinA,1), ![]() =(1,cosB),且
=(1,cosB),且 ![]() .
.
(1)求A的值;
(2)若点D在边BC上,且3 ![]() =
= ![]() ,
, ![]() =
= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且满足Sn=2﹣an , n=1,2,3,….
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=1,且bn+1=bn+an , 求数列{bn}的通项公式;
(3)设cn= ![]() ,数列{cn}的前n项和为Tn=
,数列{cn}的前n项和为Tn= ![]() .求n.
.求n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2﹣4ax+3a2<0,其中a>0; q:实数x满足 ![]() <0.
<0.
(1)若a=1,且p∨q为真,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,有一块矩形空地ABCD,AB=2km,BC=4km,根据周边环境及地形实际,当地政府规划在该空地内建一个筝形商业区AEFG,筝形的顶点A,E,F,G为商业区的四个入口,其中入口F在边BC上(不包含顶点),入口E,G分别在边AB,AD上,且满足点A,F恰好关于直线EG对称,矩形内筝形外的区域均为绿化区. 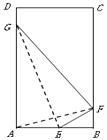
(1)请确定入口F的选址范围;
(2)设商业区的面积为S1 , 绿化区的面积为S2 , 商业区的环境舒适度指数为 ![]() ,则入口F如何选址可使得该商业区的环境舒适度指数最大?
,则入口F如何选址可使得该商业区的环境舒适度指数最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左右顶点为
的左右顶点为![]() ,右焦点为
,右焦点为![]() ,一条准线方程是
,一条准线方程是![]() ,点
,点![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 的两点,点
的两点,点![]() 为
为![]() 的中点.
的中点.
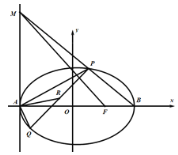
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交直线
交直线![]() 于点
于点![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)若![]() ,求直线
,求直线![]() 斜率的取值范围。
斜率的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体A1B1D1﹣ABCD中,四边形A1B1BA与A1D1DA均为直角梯形,且AA1⊥底面ABCD,四边形ABCD为正方形,AB=2A1D1=2A1B1=4,AA1=4,P为DD1的中点. 
(Ⅰ)求证:AB1⊥PC;
(Ⅱ)求几何体A1B1D1﹣ABCD的表面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com